Ряды вообще и Тейлора в частности

[_genius_]

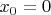
Сумма рядов $\sum\limits_{n=0}^\infty x^{6n} - \sum\limits_{n=0}^\infty x^{6n+1}$ теоретически сходится к функции $\frac{1}{1+x+x^2+x^3+x^4+x^5}$ в окрестности $x_0 = 0$, $|x - x_0| < 1$, а на деле вообще везде если по графику посмотреть, но б-г-то с ним, мб это фича Maple, т.е. он рисует 0 там где не может посчитать, а функция там как раз тоже 0. В дальнейшем ограничимся этим радиусом $|x - x_0| < 1$.

Проблема в том, что если почленно сложить эти ряды, то полученный ряд $$\sum\limits_{n=0}^\infty x^{6n}\cdot(1-x)$ к данной функции сходиться не будет причем именно в окрестности $x_0 = 0$, $|x - x_0| < 1$.

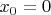
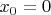
И наконец самое интересное: если взять x из радиуса сходимости $x_0 = 0$, $|x - x_0| < 1$, то что сумма рядов, что ряд полученный из почленного складывания будут выдавать одинаковые числа. В то время как на графике в тех же точках значения разные.
Что ж это за чудеса такие? Если мне не изменяет память, то почленное складывание разрешено в области сходимости рядов. Оба исходных ряда сходятся при $|x| < 1$. Так почему второй ряд не сходится к функции на графике, но сходится если подставить x из радиуса? Может с Mapl'ом что-то не так?

+Предположение: может быть ряд из почленных сумм сходится к функции поточечно, а не равномерно?

[provincialka]

Синяя линия похожа на сумму $\sum\limits_{n=0}^\infty x^{6n}$ без множителя $1-x$

-- 11.11.2014, 17:59 --

_genius_ в сообщении #929695 писал(а):

Предположение: может быть ряд из почленных сумм сходится к функции поточечно, а не равномерно?

Он же степенной! На любом отрезке из области сходимости сходится равномерно.

[_genius_]

provincialka
Вот же ж зараза, как все банально оказалось Добавил скобочки - сходится.
Благодарю, невнимательность - мое проклятье