Почитал. Оказывается, я был прав в
Шварцшильд вообще не строил ЧД - он строил гравитационное поле вокруг небесных тел, таких как Солнце, Земля и т. п. Поэтому его решение основано на том, что в области решения - вакуум, а "где-то в середине" сидит масса, со своим ТЭИ.
до последнего слова. Но всё ещё хуже. В очередной раз подтверждается, что пионерские работы - сырые. В данном случае, Шварцшильд не довёл расчёты до конца. Он построил метрику, которая сегодня хорошо известна, с переменной

но считал истинной сферической координатой переменную
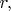
которая связана с ней как

Эта
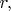
как легко видеть, обнуляется на горизонте чёрной дыры, и
поэтому Шварцшильд написал в своей работе, что разрыв метрики успешно сместился в начало координат. Однако, как известно, но ещё не обнаружено в этой работе Шварцшильда,

не является истинной сферической координатой, поскольку поперечные компоненты метрики не обращаются в нуль при

и таким образом, на этом координатном сечении образуют сферу конечной окружности и конечной площади. Для придания более физического смысла радиальной координате, её следует дефинировать так, чтобы она обнулялась вместе с длиной окружности и площадью сферы, а этому требованию удовлетворяет именно координата

Эти нюансы и не тревожили сильно Шварцшильда, поскольку для сравнения с экспериментом он рассмотрел Меркурий (вот о чём я говорил: гравитационное поле в вакууме вокруг небесных тел), и указал, что для него различие

и

имеет порядок

Выяснение же этой детали произошло, очевидно, в последующих работах, возможно, других учёных, и не попало в упомянутый сборник.