Смещение точки при масштабировании

[zm_sansan]

Пытаюсь решить такую задачу:
Начало координат лежит в точке $A$, ось $X$ направлена от $A$ к $B$, ось $Y$ от $A$ к $D$.
$ABCD$ - прямоугольник. Точка $F$, лежит, в данном случае, в произвольной области внутри прямоугольника $ABCD$, в других случаях может лежать в любом другом.

Прямоугольник $ABCD$ масштабируется относительно точки $F$ в $scale$ раз, где $scale$ положительное вещественное число. Этот прямоугольник обозначим $A_1B_1C_1D_1$.

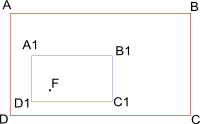
Далее внутри прямоугольника $ABCD$ выбирается произвольная точка $N$.

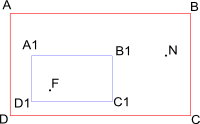
Задание1: найти соответсвующую точку $N1$ в прямоугольнике $A_1B_1C_1D_1$.

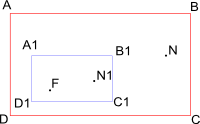
Далее всё, что внутри прямоугольника $ABCD$ мастштабируется относительно точки $F$, при этом прямоугольник $A_1B_1C_1D_1$ масштабируется до прямоугольника $ABCD$, а точка $N_1$ соответственно до точки $N$, и занимает её место. Сама же точка $N$ тоже масштабируется и занимает новую позицию.
Задание 2: найти позицию точки $N$.

ps: решаю конкретно, чтобы реализовать масштабирование в программе, но программа по моим расчётом работает не правильно, вот то ли в математике ступил, то ли в программировании, прошу помочь разобраться)

Привожу своё решение:
Задание 1:
$\overrightarrow{N_1} = \overrightarrow{F}- \overrightarrow{F}* scale + \overrightarrow{N} * scale$
Задание 2:
$\overrightarrow{N} = \overrightarrow{N_1}_{(last Image)}+ (\overrightarrow{N}_{(pre Last Image)} - \overrightarrow{N_1}_{(pre Last Image)} ) * scale$

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Тема перемещена в Карантин по следующим причинам:

1. Запишите формулы в соответствии с требованиями Правил форума, т.е. в $\TeX$.
Краткие инструкции можно найти здесь: topic8355.html и topic183.html.
Кроме этого, в теме Видео-пособия для начинающих форумчан можно посмотреть видео-ролик "Как записывать формулы".

2. Приведите свои попытки решения, по крайней мере, математическую его часть, иначе будет крайне затруднительно определить, где Вы ошиблись.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[Lia]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[upgrade]

zm_sansan в сообщении #918256 писал(а):

мастштабируется относительно точки $F$

если я правильно понимаю, масштабируете не относительно точки, а относительно сторон прямоугольника, а точка $F$ неподвижной остается.

[upgrade]

вот посмотрите, по масштабированию http://www.intuit.ru/studies/courses/70 ... 096?page=6

[zm_sansan]

upgrade
Да, точка $F$ остаётся неподвижной. Получается масштабирование происходит так, что если провести векторы $\overrightarrow{FA}$, $\overrightarrow{FB}$, $\overrightarrow{FC}$ ,$\overrightarrow{FD}$ из точки $F$, то каждый вектор умножается на величину $scale$, и новые концы векторов исходящих из точки $F$, и есть точки $A_1$, $B_1$, $C_1$, $D_1$.
Спасибо за ссылку, про масштабирование с помощью матриц я слышал, но всё таки хочется разобраться в моей задаче.

[arseniiv]

Если имеется в виду обычная гомотетия, то прямоугольники, как и получилось в ваших формулах, вообще не нужны. Просто $\overrightarrow{FN_1} = \mathrm{scale}\cdot\overrightarrow{FN}$, т. е. первая формула вся та. А вторая у вас какая-то странная. Получаться она должна аналогично, просто коэффициент растяжения будет $\mathrm{scale}^{-1}$ (или, что то же самое, заменами $N\mapsto N_2,N_1\mapsto N$).

[zm_sansan]

arseniiv
Кажется, понял, $N_{(lastImage)} = N_{(preLastImage)} / scale$
так получается?
И посмотрел, что такое гомотетия, как раз это и нужно, спасибо)
ps: точку $F$ забыл изобразить на последней картинке, но она там в том же место.

[arseniiv]

zm_sansan в сообщении #918483 писал(а):

Кажется, понял, $N_{(lastImage)} = N_{(preLastImage)} / scale$
так получается?

Как бы нет. Можете взять первое ваше уравнение и сделать там замену

arseniiv в сообщении #918465 писал(а):

$N\mapsto N_2,N_1\mapsto N$

[zm_sansan]

arseniiv
Какую точку вы обозначили за $N_2$?

[arseniiv]

Самую новую. Которая в текущих условиях вне первого прямоугольника.

[zm_sansan]

arseniiv
Т.е. $\vec{N_2} = \vec{F} + \vec{FN}/scale$

[arseniiv]

Угу.

[upgrade]

arseniiv в сообщении #918465 писал(а):

Если имеется в виду обычная гомотетия

судя по рисунку, берется отношение координат точки $F$ в СО большого прямоугольника к координатам той же точки $F$ относительно сторон малого прямоугольника и все остальные точки приводятся согласно этому отношению к координатам малого, а затем смещаются таким образом, чтобы точка $F$ осталась неподвижной.
как то так:

$F_1(x_1,y_1)=F((x_F-x_F)\cdot scale+x_F,(y_F-y_F)\cdot scale+y_F)$

$N_1(x_1,y_1)=N((x_N-x_F)\cdot scale+x_F,(y_N-y_F)\cdot scale+y_F)$

$scale=DC/D_1C_1$

т.е. сперва точка $F$ объекта помещается в начало отсчета координат вместе со всеми координатами точек объекта, затем координаты всех точек объекта умножаются на $scale$, а затем объект перемещается в точку $F$.

[arseniiv]

Так и получается обычная гомотетия ж, $\vec N = s\vec N + (1-s)\vec F = \vec F + s(\vec N - \vec F)$, где $s\equiv\mathrm{scale}$ — всё то же.