До сих пор, мы не выяснили как разлагаются простые числа

в произведение простых идеалов поля
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
.
Мы знаем только, как разлагаются простые числа

и

: они являются

-ыми степенями простых идеалов, но если

делится на

, то

.
Сейчас мы выясним, как разлагаются такие простые числа

, что

не делится на

.
Сначала покажем, что среди простых идеалов, на которые делится

в поле
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
есть идеал с нормой

.
В самом деле,

делится на

, а

не делится на

.
Следовательно

делится на некоторый простой идеал - делитель числа

.
Норма этого идеала равна

, в силу леммы 2.2 из "темы 5":
Цитата:
Лемма 2.2
--------------
Пусть

- нечётное простое число и

- простой идеал поля
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
, делящий

.
Если

делится на

, то

.
Доказательство:
----------------------
Группа по умножению

конечного поля
![$\mathbb{Z}[g]/\rho$ $\mathbb{Z}[g]/\rho$](https://dxdy-01.korotkov.co.uk/f/4/d/3/4d302a33f8ddc96522dc68a978cb7fb082.png)
является циклической.
Пусть смежный класс

является генератором группы

, где
![$a \in \mathbb{Z}[g]$ $a \in \mathbb{Z}[g]$](https://dxdy-02.korotkov.co.uk/f/9/8/7/9874819f0b30634faebb6fcf86419f7282.png)
.
Поскольку

по модулю идеала

, то

по модулю идеала

.
Следовательно,

по модулю идеала

, поскольку

не делится на

.
Следовательно,

делится на

, поскольку порядок группы

равен

.
Следовательно

, поскольку если

, где

, то

не делилось бы на

.
Что и требовалось.
Таким образом, среди простых идеалов, на которые делится

в поле
![$\mathbb{Q}[\sqrt[n]{2}]$ $\mathbb{Q}[\sqrt[n]{2}]$](https://dxdy-02.korotkov.co.uk/f/9/1/c/91c267aa7287b46623e205d06ffb45d082.png)
есть идеал с нормой

.
Что и требовалось.
Пусть

- наименьшее целое положительное число, для которого,

делится на

.
Тогда

по модулю

.
Следовательно,

по модулю

.
Обобщим процитированную лемму:
Цитата:
Лемма 2.2.1
-----------------
Пусть

- нечётное простое число и

- простой идеал поля
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
, делящий

.
Пусть

- целое положительное число.
Если

делится на

, то

делится на

.
Доказательство:
----------------------
Группа по умножению

конечного поля
![$\mathbb{Z}[g]/\rho$ $\mathbb{Z}[g]/\rho$](https://dxdy-01.korotkov.co.uk/f/4/d/3/4d302a33f8ddc96522dc68a978cb7fb082.png)
является циклической.
Пусть смежный класс

является генератором группы

, где
![$a \in \mathbb{Z}[g]$ $a \in \mathbb{Z}[g]$](https://dxdy-02.korotkov.co.uk/f/9/8/7/9874819f0b30634faebb6fcf86419f7282.png)
.
Поскольку

по модулю идеала

, то

по модулю идеала

.
Следовательно,

по модулю идеала

, поскольку

не делится на

.
Следовательно,

делится на

, поскольку порядок группы

равен

.
Что и требовалось.
Мы показали, что

по модулю

.
Значит, норма любого простого идеала

- делителя числа

- равна

, где

.
Если
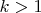
, то

, в силу леммы 2.3 из темы 5:
Цитата:
Лемма 2.1
---------------
Пусть

- нечётное простое число и

- простой идеал поля
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
, делящий

.
Пусть

не делится на

, где

- целое положительное число.
Если

, то

делится на

.
Доказательство:
---------------------
Пусть

.
Тогда

делится на

, в силу малой теоремы Ферма для идеалов.
Имеем:

.
Заметим, что второе равенство имеет место, поскольку

не делится на

и

не делится на

.
Значит:
(10)

.
Если обозначить

и

, то правая часть равенства (10), равная

, сравнима с

по модулю

.
Следовательно, правая часть равенства (10) сравнима с

по модулю

, поскольку число

сравнимо с

по модулю

.
Следовательно, левая часть равенства (10) не делится на

.
Следовательно,

не делится на

.
Следовательно,

делится на

, поскольку

делится на

.
Что и требовалось.
Лемма 2.3
--------------
Пусть

- нечётное простое число и

- простой идеал поля
![$\mathbb{Q}[g]$ $\mathbb{Q}[g]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a24599daab8efe13972cceb995fdc982.png)
, делящий

.
Пусть

не делится на

, где

- целое положительное число.
Если
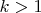
, то

.
Доказательство:
----------------------
Предположим обратное, что

, где
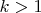
.
Тогда

делится на

, в силу леммы 2.1, следовательно

в силу леммы 2.2.
Это противоречит предположению, что

.
Таким образом, для любого простого идеала

- делителя числа

: либо

,
либо

, где

- наименьшее целое положительное число, для которого,

делится на

.
Мы показали, что существует такой простой идеал

, что

.
Но, чтобы в разложении числа

было более одного такого идеала

- это вряд ли.
Дело в том, что

, поскольку

не делится на

.
Если количество таких простых идеалов

, что

, равно

, то

делится на

.
Если

, то

, поскольку

делится на

.
Нам известны всего 2 таких простых числа

, что

делится на

.
Чтобы

делилось на

- это вряд ли, хотя доказать я это не могу.
Не исключено, что существует другое доказательство единственности идеала

, с

.