==Введение==
При регистрации (измерении) квантовых частиц всевозможные усилители сигнала, так как энергия взаимодействия отдельной частицы с окружением слишком мала чтобы частицу можно было заметить непосредственно. Возникает вопрос связанны ли странные свойства квантовых измерений с "чрезмерным усилением" используемых нами детекторов квантовых частиц? Такие странные свойства, как "коллапс" волновой функции частицы при измерении и необратимость измерений. Кто-то из физиков говорит, что свойства измерений не связаны с "чрезмерным усилением", то есть свойства диктуются постулатами копенгагенской интерпретации квантовой механики, и не откуда не выводятся. Кто-то подозревает что такая связь есть.
Однако связь между "коллапсом" Вф и "чрезмерным усилением" можно показать из
совершенно элементарнейших достаточно простых рассуждений. И даже, как оказалось, "коллапс" ВФ происходит как раз из-за "чрезмерного усиления" - скачка энтропии в детекторе квантовых частиц.
Для начала рассмотрим простую энергетическую модель детектора.
==модель детектора==
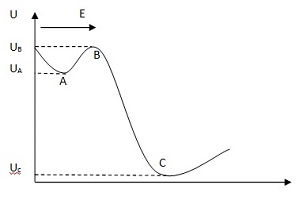
На пути частицы помещается детектор, находящийся в метастабильном состоянии

локального равновесия. Частица взаимодействуя с детектором может, либо обогнуть детектор - не измериться, либо перевести детектор в нестабильное состояние

, из которого детектор переходит в состояние глобального минимума

. При переходе из

в

детектор высвобождает запасенную в нем энергию в тепло или вспышку света (или электрический ток). В зависимости от устройства детектора наблюдатели (экспериментаторы) определяют, что измерение произошло по макроскопическим различимым: состоянию

, вспышке света, току. Детектор усиливает сигнал (информацию) от частицы до макроскопических значений.
Если при событии

- "чрезмерном усилении" всегда происходит событие

- коллапс ВФ, логично предположить, что события

и

как-то связаны. То есть, можно предположить, что "чрезмерное усиление" связано с коллапсом ВФ. Но как связано?
Отличие детекторов от недетекторов, например стекла, в том что при переходе

в

высвобождается большая порция энергии. Большая порция потенциальной энергии переходит в кинетическую. При резком быстром переходе потенциальной энергии в кинетическую, как правило значительная часть энергии рассеивается в тепло (не строгое утверждение, интуитивное, но надеюсь понятное. Много энергии - много уходит в тепло). Таким образом при измерении в детекторе происходит относительно большой скачок энтропии.
Возможно коллапс ВФ связан со скачком энтропии? Рассмотрим существующие теории квантовых измерений.
==Ограниченный интеграл по траекториям. Квантовый коридор==
В статье
М.Б. Менский. Явление декогеренции и теория непрерывных квантовых измерений вводиться понятие квантовый коридор.

Нечеткое измерение описывается интегралом по путям, ограниченном квантовым коридором, в виде:
![$U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} \int_{0}^{t}(p\dot{q}-H(p,q,t) )dt - k\int_{0}^{t}(A(p,q,t)-a(t))^{2}dt \right\}}$ $U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} \int_{0}^{t}(p\dot{q}-H(p,q,t) )dt - k\int_{0}^{t}(A(p,q,t)-a(t))^{2}dt \right\}}$](https://dxdy-02.korotkov.co.uk/f/9/8/b/98b11e2c681e05a34e908bf00103418e82.png)
коэффициент

характеризует "силу измерения", его точность. Его можно представить в виде:

где

погрешность непрерывного измерения, длящегося в течении времени

.
коэффициент

пропорционален числу частиц окружения измеряемой квантовой системы (не нашел точной формулы. Похоже он в другой статье её приводил. Но не важно. Здесь просто разоряюсь на описание пути идеи. Гипотеза связи измерения с энтропией на этом коэффициенте проявилась). Чем больше степеней свободы взаимодействует, тем больше

. И этим он похож на энтропию.
Возникает идея, что если описывать измерения функционалом:
![$U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} \int_{0}^{t}(p\dot{q}-H(p,q,t) )dt - f(S) \right\}}$ $U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} \int_{0}^{t}(p\dot{q}-H(p,q,t) )dt - f(S) \right\}}$](https://dxdy-03.korotkov.co.uk/f/2/3/b/23b2c549685a24badadbb243d659ff8c82.png)
(1)
где f(S) какая-то функция от энтропии?
Тогда при скачке энтропии "сила измерения" резко увеличивается и квантовый коридор резко сужается. Частица локализуется в области скачка энтропии. На детекторе. Коллапс ВФ.
==функционал по путям с энтропией==
Как оказалось функционал по путям с энтропией уже выведен из Бомовской интерпретации квантовой механики в статье
В.И. Сбитнев Бомовские траектории и парадигма интегрирования по путям. Комплексная Лагранжева механика. В формулах (32) (34а) (34б) статьи. Рассмотрим формулу (32) статьи.

(2)
где

обозначено действие системы, а

её энтропия.
Интегрирую формулу (32) по всевозможным путям развития системы, получим функционал по путям с энтропией.
![$U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} J - S \right\}}$ $U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} J - S \right\}}$](https://dxdy-04.korotkov.co.uk/f/3/f/f/3ff0b0616a51c48356f43d01ba47decb82.png)
(3)
В функционале по путям (3) энтропия определяет квантовый коридор системы. Различные пути системы войдут в интеграл по путям с весом

Правда, как ни странно, состояния с большей энтропией входят в интеграл по путям с меньшим весом! Это означает, что состояния с большей энтропией менее вероятны, чем состояния с меньшей энтропией. Здесь прямое противоречие со вторым началом термодинамики:
Состояния макроскопической системы с большей энтропией, более вероятны, чем состояния с меньшей энтропией.
В справедливости формулы (3) нет смысла сомневаться. Её можно вывести элементарно из принципа сложения амплитуд ВФ.

![$U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} J - S \right\}}=\int{d[p]d[q]\vert \rho(q,p,t) \vert \exp\left\{\frac{i}{\hbar} J \right\}}$ $U^{[a]}_{T}(q'',q')=\int{d[p]d[q]\exp\left\{\frac{i}{\hbar} J - S \right\}}=\int{d[p]d[q]\vert \rho(q,p,t) \vert \exp\left\{\frac{i}{\hbar} J \right\}}$](https://dxdy-01.korotkov.co.uk/f/4/9/a/49a0f96283add5be9c5184e2b0d9449982.png)
(4)
Таким образом интеграл по путям с энтропией как раз и реализует принцип сложения амплитуд ВФ. А вот интеграл по путям Фейнмана суммирует только фазы.
Второе начало термодинамики бесчисленное множество раз подтверждено экспериментально. В принципе сложения амплитуд ВФ тоже никто не сомневается. Почему они противоречат друг другу?
==Источник порядка==
Чтобы разобраться с этим противоречием найдем вероятность суперпозиции

ВФ, отнесенных к

различным путям:

Первый член ур-ния

- это сумма вероятностей. То есть её можно рассматривать как классическую статсумму. Как известно, она максимальна когда энтропия системы максимальна. Этот член ур-ния выражает второе начало термодинамики.
Второй член ур-ния

максимален, когда

близко к

. То есть, когда действие близко к минимуму (

пока отложим). Этот член ур-ния выражает принцип наименьшего действия. Он максимален когда квантовая система наиболее когерентна.
В общем случае, максимумы вероятности образуемые максимом энтропии и минимумом действия
не совпадают ( Энтропия максимальна при полной декогерентности системы, а действие минимально в когерентном состоянии). В общем случае, не совпадение максимумов вероятности порождает
конкуренцию между ними. Энтропия и действие "боряться" за максимум вероятности. За проявление в наблюдаемом нами мире.
Таким образом, принцип минимума действия антагонист принципа максимума энтропии. Так как принцип максимума энтропии иногда называют принципом Хаоса или Источником Хаоса, принцип минимума действия можно назвать принципом Порядка или Источником Порядка.
Так как, принцип минимума действия равноценен принципу максимума энтропии, второе начало термодинамики обобщается в следующий принцип:
Термодинамическая система выведенная из состояния равновесия стремиться в ближайшее состояние с минимумом действия и максимумом энтропииЭтот принцип можно назвать принципом минимакса действия-энтропии (ну или принцип ИньЯнь). Равновесное состояние определяется точкой минимакса действия-энтропии.
==Минимакс действия-энтропии в квантовых измерениях==
Вернемся к квантовым измерениям. Когда ВФ частицы встречает на своем пути детектор квантовых частиц, с большим возможным скачком энтропии, возникает борьба между двумя максимумами вероятности.
Первый максимум вероятности. Квантовая система детектор+частица может перейти в состояние с большей энтропией и соответственно с большей вероятностью существования.
Второй максимум вероятности. Квантовая частица может сохранить свой максимум когерентности в пространстве.
Борьба между двумя максимумами вероятности измериться и неизмериться хорошо и полно описывают поведение квантовых систем при измерениях на качественном уровне.
==Выводы и следствии==
Связь между "коллапсом" Вф и "чрезмерным усилением" - скачком энтропии в детекторе показана на качественном уровне. (Цель статьи достигнута. Извинюсь за корявое изложение. Стиль изложения еще шлейфовать и щлейфовать). Попутно обобщено второе начало термодинамики (Вот уж никак не ожидал!!!).
Из обобщенного второго второго начала термодинамики следует возможность существования Вечного двигателя (Четно слово не хотел я его изобретать!!! Сам как-то вылез...). Выведенная из равновесия термодинамическая система следует в
ближайшую точку минимакса действия-энтропии. Ближайшая - это не обязательно состояние с большей энтропией. Если получиться создать цепочку...
В статье, неявно, предполагалось что ВФ скалярная величина

. Тогда как, для частиц со спином, плотность вероятности является матрицей, а энтропия - функция от следа матрицы плотности вероятности. В виду общности принципов минимума действия и максимума энтропии, обобщенное второе начало термодинамики весьма вероятно так же справедливо и для частиц со спином. Но естественно необходимо дополнительное исследование. Бозоны - частицы с целым спином при низкой температуре предпочитают находиться в одном когерентном состоянии, а фермионы в "декогерентных" состояниях. Это как-то связано с минимаксом энтропии?!!
==Литература==
М.Б. Менский. Явление декогеренции и теория непрерывных квантовых измеренийВ. Зурек. ДЕКОГЕРЕНЦИЯ И ПЕРЕХОД ОТ КВАНТОВОГО МИРА К КЛАССИЧЕСКОМУФеноменологическая модель квантовых измеренийВ.Э. ТЕРЕХОВИЧ ФИЛОСОФСКО-МЕТОДОЛОГИЧЕСКИЕ ПРОБЛЕМЫ ПРИНЦИПА НАИМЕНЬШЕГО ДЕЙСТВИЯВ.И. Сбитнев Бомовские траектории и парадигма интегрирования по путям. Комплексная Лагранжева механика-- Ср сен 17, 2014 07:34:01 --В принципе в статье я уверен, но есть несколько слабых мест.
При резком быстром переходе потенциальной энергии в кинетическую, как правило значительная часть энергии рассеивается в тепло (не строгое утверждение, интуитивное, но надеюсь понятное. Много энергии - много уходит в тепло)
Полностью интуитивное предположение :(
Первый член ур-ния

- это сумма вероятностей. То есть её можно рассматривать как классическую статсумму. Как известно, она максимальна когда энтропия системы максимальна.
Здесь непроверенное утверждение. Нужно добраться проверить...
Тогда при скачке энтропии "сила измерения" резко увеличивается и квантовый коридор резко сужается. Частица локализуется в области скачка энтропии. На детекторе. Коллапс ВФ.
К сожалению ошибка :(.
Правда, как ни странно, состояния с большей энтропией входят в интеграл по путям с меньшим весом!
Противоречие однако :). Вроде как "до" измерения волновой пакет размывается, а коллапс уже после "после" измерения.
Нехорошо смешиваются понятия статсумма так сказать по "путям" и статсумма состояний на момент времени.
Есть какие-нибудь подсказки как более четко описать?
