2-й Всеукраинский турнир математических боев им. М.И.Ядренко
Киев
Математический бой №2
30.10.2007
Младшая лига
1. Задан остроугольный треугольник

.

~--- центр описанной окружности, Н~--- ортоцентр, и
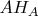
,
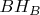
,
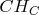
~--- высоты

. Обозначим через

,

,

~--- центры окружностей, описанных около треугольников
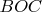
,

и
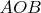
соответственно. Доказать, что прямые

,

,

пересекаются в однои точке, лежащей на прямой Эйлера

. Прямой Эйлера треугольника является прямая, соединяющая центр описанной окружности и центр тяжести треугольника.
2. Выпуклый шестиугольник

удовлетворяет следующим условиям:\\
1)

,

,

;\\
2) расстояния между этими парами параллельных прямих~--- одинаковые;\\
3)

.\\
Доказать, что диагонали

и

шестиугольника пересекаются под углом

.
3. На доске один или несколько раз подряд записали натуральное число

в десятичной записи и получили двоичную запись того самого числа

. Найдите все возможные значения

.
4. Восемь команд разыгрывают первенство в один круг, т.\,е. каждая команда играет с каждой другой 1 раз, при этом расписание соревнования составлено по турам~--- в каждом туре играет каждая команда. Через какое наименьшее количество туров с начала чемпионата могут быть уже известны команды, занявшие первое и последнее места (т.\,е. при любых других результатах в оставшихся турах эти команды все равно наберут наибольшее и наименьшее количество очков в строгом понимании), если это было:\\
а) первенство по волейболу, где за победу команда получает 1 очко, за поражение~--- 0 очков и
ничьих не бывает;\\
б) первенство по гандболу, где за победу команда набирает 2 очка, за поражение~--- 0 очков, за
ничью каждая команда набирает 1 очко?
5. Найти количество пар натуральных чисел

, удовлетворяющих уравнению

(

-факториал~--- это число

).
6. Задан граф с

вершинами. Доказать, что можно ввести ориентацию на его ребрах таким образом, чтобы модуль разности между количествами ребер, входящих в вершину и выходящих из нее, не превышал единицы.
7. Решить систему уравнений:

8. Для произвольных неотрицательных чисел

,

,

доказать неравенство:

9. Найти все множества

, которые содержат по крайней мере два числа и таких, что для каждых двух
разных

число

(

~--- НОД чисел

,

).
10. Последовательность чисел

задается по правилу:

,

,

. Доказать, что все члены последовательности~--- целые числа.
Математический бой №2
30.10.2007
Старшая лига
1. Задан остроугольный треугольник

.

~--- центр описанной окружности, Н~--- ортоцентр, и
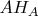
,
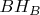
,
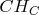
~--- высоты

. Обозначим через

,

,

~--- центры окружностей, описанных около треугольников
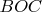
,

и
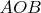
соответственно. Доказать, что прямые

,

,

пересекаются в одной точке, лежащей на прямой Эйлера

. Прямой Эйлера треугольника является прямая, соединяющая центр описанной окружности и центр тяжести треугольника.
2. Точка

выбрана на стороне

треугольника

. На сторонах

и

выбраны точки

,

соответственно таким образом, что

. Найти геометрическое место точек

~--- середин отрезков

, для всех возможных пар точек

,

.
3. Последовательность вещественных чисел

задана рекуррентно:

,

. Доказать, что существует натуральное

, для которого

.
4.

~--- простое число и множество

. Пусть

~--- вершины правильного

-угольника,

~--- его центр. Найти все подмножества

, для которых выполняется равенство:

.
5. Задана квадратная таблица

. В каждой ячейке этой таблицы записан <<0>> или <<1>>. Сколько существует способов расставить эти числа так, чтобы произведение каждых двух чисел, записанных в ячейках с общей стороной, было равно 0.
6. Пусть множество

. Функция
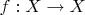
определена следующим образом:

,

,

,

. Существует ли

такое, что для любого

существует

такое, что

\,?
7. Найти все множества

, которые содержат по крайней мере два числа и таких, что для каждых двух
разных

число

(

~--- НОД чисел

,

).
8. В треугольнике

с углом

проведены биссектрисы

и

. Доказать, что

.
9. Решить уравнение:

10. На доске один или несколько раз подряд записали натуральное число

в десятичной записи и получили двоичную запись того самого числа

. Найдите все возможные значения

.
Начало здесь:
http://dxdy.ru/viewtopic.php?t=9720
http://dxdy.ru/viewtopic.php?t=9732



