Нашёл хивариантам занятное применение...
Рассмотрим двумерное пространство Минковского

и перейдём в нём к риндлеровым координатам
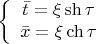
в которых интервал принимает вид

Я не буду говорить много слов об этих хорошо известных координатах. Желающие подробностей и картинок, могут сходить
сюда.
Так вот. Цель у меня будет такая: имея перед собой только

проломиться сквозь горизонт
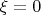
до состояния

, причём не абы как, а действуя рутинно и однообразно и никаких замен с потолка не угадывая. А помогут мне в этом следующие величины:
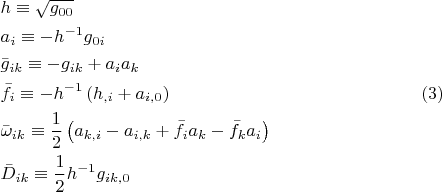
Посчитав их для

, обнаружим, что на горизонте имеются проблемы:
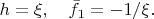
Это значит, что систему тел отсчёта надобно менять. Для этого совершим простейшее НЕхронометрическое преобразование
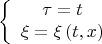
что даст нам следующий интервал
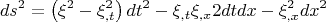
Снова вычислим

. Особого внимания из них требуют следующие
![$$\[
\begin{gathered}
h = \sqrt {\xi ^2 - \xi _{,t}^2 } \hfill \\
\bar f_1 = - \frac{{\xi \xi _{,x} \left[ { - 2\xi _{,t}^2 + \xi \left( {\xi + \xi _{,tt} } \right)} \right]}}
{{\left( {\xi ^2 - \xi _{,t}^2 } \right)^2 }} \hfill \\
\bar g_{11} = \frac{{\xi ^2 \xi _{,x}^2 }}
{{\xi ^2 - \xi _{,t}^2 }} \hfill \\
\bar D_{11} = \frac{{\xi \xi _{,x} \left[ {\xi \left( {\xi ^2 - \xi _{,t}^2 } \right)\xi _{,tx} + \xi _{,x} \left( { - \xi _{,t}^3 + \xi \xi _{,t} \xi _{,tt} } \right)} \right]}}
{{\left( {\xi ^2 - \xi _{,t}^2 } \right)^{{5 \mathord{\left/
{\vphantom {5 2}} \right.
\kern-\nulldelimiterspace} 2}} }} \hfill \\
\end{gathered}
\]
$$ $$\[
\begin{gathered}
h = \sqrt {\xi ^2 - \xi _{,t}^2 } \hfill \\
\bar f_1 = - \frac{{\xi \xi _{,x} \left[ { - 2\xi _{,t}^2 + \xi \left( {\xi + \xi _{,tt} } \right)} \right]}}
{{\left( {\xi ^2 - \xi _{,t}^2 } \right)^2 }} \hfill \\
\bar g_{11} = \frac{{\xi ^2 \xi _{,x}^2 }}
{{\xi ^2 - \xi _{,t}^2 }} \hfill \\
\bar D_{11} = \frac{{\xi \xi _{,x} \left[ {\xi \left( {\xi ^2 - \xi _{,t}^2 } \right)\xi _{,tx} + \xi _{,x} \left( { - \xi _{,t}^3 + \xi \xi _{,t} \xi _{,tt} } \right)} \right]}}
{{\left( {\xi ^2 - \xi _{,t}^2 } \right)^{{5 \mathord{\left/
{\vphantom {5 2}} \right.
\kern-\nulldelimiterspace} 2}} }} \hfill \\
\end{gathered}
\]
$$](https://dxdy-03.korotkov.co.uk/f/2/b/1/2b18844dd03129efdaee65ed9441b97982.png)
Первым делом избавимся от силы инерции, положив
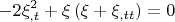
Интегрируя разок, получим
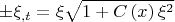
откуда сразу же следует выражение
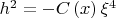
, показывающее, что

должно быть отрицательно. Поэтому положим
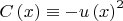
, где

не обращается в нуль.
Интегрируя далее, находим
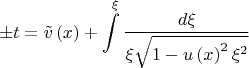
Интеграл легко берётся
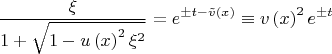
где

- ещё одна некоторая не обращающаяся в нуль функция.
Разрешая относительно
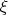
, находим
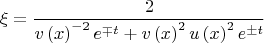
Этому выражению можно придать более симпатичный вид
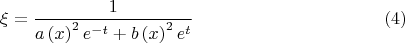
гже

и

уже традиционно некоторые и не обращающиеся в нуль функции.
Снва посчитав

, убеждаемся, что
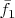
, как ему и полагается, обнулился, а остальные потенциально проблемные величины приняли вид
![$$\[
\begin{gathered}
h = \frac{{2ab}}
{{\left( {a^2 e^{ - t} + b^2 e^t } \right)^2 }} \hfill \\
\bar g_{11} = \frac{{\left( {aa'e^{ - t} + bb'e^t } \right)^2 }}
{{a^2 b^2 \left( {a^2 e^{ - t} + b^2 e^t } \right)^2 }} \hfill \\
\bar D_{11} = \frac{{\left( {ab' - ba'} \right)\left( {aa'e^{ - t} + bb'e^t } \right)}}
{{a^2 b^2 \left( {a^2 e^{ - t} + b^2 e^t } \right)}} \hfill \\
\end{gathered}
\]
$$ $$\[
\begin{gathered}
h = \frac{{2ab}}
{{\left( {a^2 e^{ - t} + b^2 e^t } \right)^2 }} \hfill \\
\bar g_{11} = \frac{{\left( {aa'e^{ - t} + bb'e^t } \right)^2 }}
{{a^2 b^2 \left( {a^2 e^{ - t} + b^2 e^t } \right)^2 }} \hfill \\
\bar D_{11} = \frac{{\left( {ab' - ba'} \right)\left( {aa'e^{ - t} + bb'e^t } \right)}}
{{a^2 b^2 \left( {a^2 e^{ - t} + b^2 e^t } \right)}} \hfill \\
\end{gathered}
\]
$$](https://dxdy-04.korotkov.co.uk/f/b/0/8/b08fb5b831374781e05181b444fa36b282.png)
Мы видим, что дальнейшее упрощение возможно за счёт
изничтожения нестационарности пространственной метрики. Для чего достаточно положить

. Что даст следующий вид искомой нами функции перехода
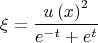
В этом месте у меня кончились буквы, поэтому давайте сделаем вид, что функция

появляется здесь впервые (свойства её можно брать старые).
После такой замены интервал примет вид
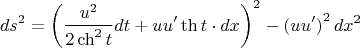
Дальше напрашивается
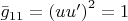
, для чего положим

и окончательно получим
![$$\[
\begin{gathered}
\xi = \frac{{2x}}
{{e^{ - t} + e^t }} \hfill \\
ds^2 = \left( {\frac{x}
{{\operatorname{ch} ^2 t}}dt + \operatorname{th} t \cdot dx} \right)^2 - dx^2 \hfill \\
\end{gathered} \eqno (5)
\]
$$ $$\[
\begin{gathered}
\xi = \frac{{2x}}
{{e^{ - t} + e^t }} \hfill \\
ds^2 = \left( {\frac{x}
{{\operatorname{ch} ^2 t}}dt + \operatorname{th} t \cdot dx} \right)^2 - dx^2 \hfill \\
\end{gathered} \eqno (5)
\]
$$](https://dxdy-01.korotkov.co.uk/f/c/2/2/c22aa05f90213e967350ba759f62a8fe82.png)
Выглядит страшновато?

Однако, те из величин

, которые имеют физический смысл, ведут себя просто прекрасно! Но, чтобы это увидеть, нужно совершить на этот раз
хронометрическое преобразование, не меняющее хивариантов (а чего их менять, коль они и так замечательные?)
Итак, выполним хронометрическое преобразование
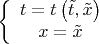
после которого интервал

примет угадайте что? Правильно, вид:
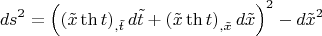
Осталось потребовать
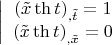
и мы получим
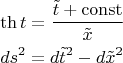
Вуаля.
P.S. Для Шварцшильда такой подход тоже работает. Когда-нибудь наберусь духу и попробую провернуть для Керра.