Упражнение из Колмогорова Фомина (Глава III $3)

[Camush]

Доброго времени суток!

Читаю книгу "Элементы теории функций и функционального анализа" Колмогорова Фомина (шестое издание, Москва "Наука", 1989) и решаю упражнения, приведённые в книге. Некоторые упражнения не получается решить, или я не полностью уверен в правильности своего решения, поэтому обращаюсь к вам на форум за помощью и советом.

Упр.1 (стр. 166, Глава III Нормированные и топологические линейные пространства $3 Нормированные пространства)
2) Приведите пример последовательности вложенных непустых ограниченных замкнутых выпуклых множеств в некотором B-пространстве (банаховом пространстве), имеющих пустое пересечение.

Решение:

Построим такое банахово пространство $R$ следующим образом: на числовой прямой $\mathbb R$ выберем точку $a$ и заменим её на точку $A$, то есть $R=\mathbb R\setminus\{a\}\cup\{A\}$.
Все окрестности точки $A$ - есть в точности окрестности точки $a$, однако $A\not=a$.
В качестве выше упомянутой последовательности возьмём интервалы $I_k(a+1/k,2/k)$ с центром в точке $a+1/k$ и длиной $2\cdot2/k$. Пересечение всех интервалов даст точку a, которая не принадлежит $R$, следовательно пересечение пусто.

Графически это можно представить так:



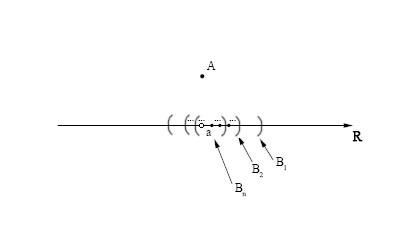
Уважаемые форумчане, правильно ли такое решение? Есть ли более наглядное решение?

Заранее спасибо за ответ!

[Oleg Zubelevich]

$A_n=\{x=\{x_i\}\in c_0\mid x_s=1,\quad s=1,\ldots n,\quad\|x\|\le 1\}$

[Deggial]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
Причина переноса: формулы не оформлены $\TeX$ом

Camush

Camush в сообщении #888120 писал(а):

на числовой прямой R выберем точку a и заменим её на точку А.
Пусть R=R\{a}U{A}.

Наберите все формулы и термы $\TeX$ом.
Инструкции по оформлению формул здесь или здесь (или в этом видеоролике).
См. также тему Что такое карантин, и что нужно делать, чтобы там оказаться.
После исправлений сообщите в теме Сообщение в карантине исправлено, и тогда тема будет возвращена.

Camush в сообщении #888120 писал(а):

P.S.: есть ещё несколько вопросов по решению некоторых упражнений из этой книги, буду их публиковать в этой теме

Не надо. Новые задачи оформляйте в виде новых тем.

[Toucan]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»

[Camush]

Oleg Zubelevich в сообщении #888142 писал(а):

$A_n=\{x=\{x_i\}\in c_0\mid x_s=1,\quad s=1,\ldots n,\quad\|x\|\le 1\}$

Объясните, пожалуйста, что у вас означает $c_0$ И из описания множества $A_n$ следует понимать, что для каждого $i$ выбирается одно какое-то $s$? Но тогда разве эти множества будут образовывать последовательность вложенных друг в друга множеств?

[mihaild]

Camush в сообщении #889511 писал(а):

Oleg Zubelevich в сообщении #888142 писал(а):

$A_n=\{x=\{x_i\}\in c_0\mid x_s=1,\quad s=1,\ldots n,\quad\|x\|\le 1\}$

Объясните, пожалуйста, что у вас означает $c_0$ И из описания множества $A_n$ следует понимать, что для каждого $i$ выбирается одно какое-то $s$? Но тогда разве эти множества будут образовывать последовательность вложенных друг в друга множеств?

$c_0$ - пространство стремящихся к нулю последовательностей с покоординатными сложением и умножением на скаляр, и супремум нормой, т.е. $\|x\| = \max{|x_n|}$ (т.к. последовательность стремится к нулю, то супремум достигается).

В качестве $A_n$ берутся последовательности, первые $n$ координат которых равны $1$, а все остальные не превосходят по модулю единицу. Их пересечение пусто.

В Вашем же решении не очень понятно, какое банахово пространство Вы рассматриваете - как задаются линейная структура и норма?

[Camush]

mihaild в сообщении #889517 писал(а):

$c_0$ - пространство стремящихся к нулю последовательностей с покоординатными сложением и умножением на скаляр, и супремум нормой, т.е. $\|x\| = \max{|x_n|}$ (т.к. последовательность стремится к нулю, то супремум достигается).

В качестве $A_n$ берутся последовательности, первые $n$ координат которых равны $1$, а все остальные не превосходят по модулю единицу. Их пересечение пусто.

Спасибо, теперь всё понятно!

mihaild в сообщении #889517 писал(а):

В Вашем же решении не очень понятно, какое банахово пространство Вы рассматриваете - как задаются линейная структура и норма?

Мой подход, наверное, несколько топорный. В нём рассматривается пространство построенное на основе вещественной прямой $\mathbb R$ (с заменой одной точки $a\in\mathbb R$ на другую $A\notin\mathbb R$, исключая вариант отождествления) строится банахово пространство с обычной нормой на основе евклидовой метрики. Чтобы не возникало проблем с вновь введённой точкой $A$, все окрестности удалённой точки $a$ - объявляются в точности окрестностями точки $A$, и при предельном переходе точка $a$ просто заменяется на $A$.
Не совсем понимаю термин "линейная структура"... Погуглил... Похоже Вы имеете в виду "метрика", тогда я уже ответил на Ваш вопрос выше.
При таком подходе имеет ли право на существование мое решение?

[deep down]

Camush, у меня вопросы по Вашему решению остались. Построенное пространство должно быть линейным. Если вектор $1\in R$, то умножим его на скаляр $a$, получим $a\in R$. И добавленный вектор $A$ тоже можно умножать на все скаляры. Ещё раз проверьте, что операции корректно заданы.
Ну и пример от себя в духе уже указанного, только в гильбертовом пространстве.
Пусть $A = \{(x_1,x_2,...)|x_i\ge 0, \sum_{i=1}^\infty x_i = 1\}$. Тогда определим $A_n = \{x\in A|x_1=...=x_n=0\}$

[Oleg Zubelevich]

А в гильбертовом пространстве, и вообще, в рефлексивном пространстве такого примера быть не может. Потому, что замкнутое ограниченное выпуклое подмножетво рефлексивного пространства слабо компактно. А пересечение вложенных друг в друга компактов непусто.

[Camush]

mihaild в сообщении #889517 писал(а):

Camush в сообщении #889511 писал(а):

Oleg Zubelevich в сообщении #888142 писал(а):

$A_n=\{x=\{x_i\}\in c_0\mid x_s=1,\quad s=1,\ldots n,\quad\|x\|\le 1\}$

Объясните, пожалуйста, что у вас означает $c_0$ И из описания множества $A_n$ следует понимать, что для каждого $i$ выбирается одно какое-то $s$? Но тогда разве эти множества будут образовывать последовательность вложенных друг в друга множеств?

$c_0$ - пространство стремящихся к нулю последовательностей с покоординатными сложением и умножением на скаляр, и супремум нормой, т.е. $\|x\| = \max{|x_n|}$ (т.к. последовательность стремится к нулю, то супремум достигается).

В качестве $A_n$ берутся последовательности, первые $n$ координат которых равны $1$, а все остальные не превосходят по модулю единицу. Их пересечение пусто.

Это правильное решение

Всем спасибо за помощь, я разобрался!

[deep down]

В моём примере лучше было поставить условие $\sum_i x_i^2=1$. А в остальном проблем не вижу.
Oleg Zubelevich, пожалуйста, уточните. Множества $A_n$ будут предкомпактны в слабой топологии, но вот слабое замыкание включает точки с условием $\sum_i x_i^2\le 1$. Пока не вижу, как указанyые теоремы запрещают эффект в $L_2$.

Camush, пара слов про то, как мы получили решения. Дело в некомпактности единичного шара в бесконечномерном пространстве. В $\mathbb{R}^n$ с ограниченными множествами такое потребует "открытости", тут Вы смотрели в правильную сторону. А вот в бесконечномерном случае множества можно сделать замкнутыми, а "открытость" направить в бесконечность по размерностям. Объяснил коряво, но надеюсь, что на других примерах понимание придёт.

[Oleg Zubelevich]

ну я не знаю какиеми еще словами объяснять.

вот условие задачи:

Camush в сообщении #888120 писал(а):

Приведите пример последовательности вложенных непустых ограниченных замкнутых выпуклых множеств в некотором B-пространстве (банаховом пространстве), имеющих пустое пересечение.

вот комментарий:

Oleg Zubelevich в сообщении #890337 писал(а):

в гильбертовом пространстве, и вообще, в рефлексивном пространстве такого примера быть не может. Потому, что замкнутое ограниченное выпуклое подмножетво рефлексивного пространства слабо компактно. А пересечение вложенных друг в друга компактов непусто.

мне добавить больше нечего

[deep down]

А-а, теперь понял. Вы правы, упустил из виду выпуклость. Поэтому такой пример получится в $l_1$, но не в рефлексивных $L_p$. Спасибо.