Некоторые вопросы по матстатистике

[ShMaxG]

Навеяно последними постами темы topic85916.html

В учебнике Ивченко, Медведев "Введение в математическую статистику" в главе 3 про общую теорию оценивания неизвестных параметров распределений на стр.161 подчеркивается, что

Цитата:

при оценивании заданной параметрической функции $\tau(\theta)$ необходимо, чтобы область значений соответствующей оценки $T(X)$ совпала с областью значений $\tau(\theta)$, так как в противном случае оценка может давать значения вообще не принимаемые оцениваемой величиной (оценка будет лишена практического смысла!)

Но позвольте, они вводят, например, на стр.35 статистическую модель $\text{Bi}(k,\theta)$ при $0 < \theta < 1$, и при этом говорят об эффективной оценке параметра $\theta$ равной $\bar X / k$, которая с ненулевой вероятностью может принимать значение 0 и 1.

Это еще не вся беда. В разделе про оценку максимального правдоподобия (ОМП) на стр.230 в качестве условия в теореме про состоятельность и асимптотическую нормальность ОМП указано, что при любых $x$ из выборочного пространства оценка должна лежать внутри параметрического множества. С учетом моего замечания, ОМП $\bar X / k$ может с ненулевой вероятностью попадать и на границу параметрического множества. На этих границах вклад выборки не существует, так как логарифмы в бесконечность обращаются. И получается как бы, что эту теорему для этой простой такой ОМП не применить.

Странности попадаются и дальше, в "комментариях к свойствам ОМП" на стр. 232. Они берут пуассоновскую модель и рассматривают статистику $1/ \bar X$. Но это не случайная величина, так как $\bar X$ может принять значение 0 с ненулевой вероятностью (что там и замечено).

Помогите прояснить ситуацию, может я чего-то я не замечаю и не понимаю?

[ShMaxG]

Странно, что никто не отписался в теме, уж слишком явные вылезли несостыковки. После некоторого перерыва я посмотрел разные книжки/лекции/статьи, и вот что уяснил (надеюсь, что меня поправят, если я не прав, либо добавят свое видение).

1. Область значений оценки не обязана совпадать с областью значений оцениваемой параметрической функции. Об этом написано в Леман Э., "Теория точечного оценивания". Там сказано, что "удобно не накладывать это ограничение". Видимо это делается для теоретических выкладок и доказательств. Вообще такого требования я в книжках почти не встречал. 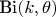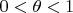Так что можно совершенно спокойно (это даже очень удобно) вводить статистическую модель $\text{Bi}(k,\theta)$ при $0 < \theta < 1$ и рассматривать статистику $\bar X / k$.

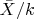
2. Далее насчет определения оценки ОМП. В лекциях MIT (http://ocw.mit.edu/courses/mathematics/ ... ure-notes/) я обнаружил более аккуратное, на мой взгляд, определение:

3.1 Maximum Likelihood Estimates - In Exponential Families писал(а):

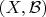
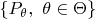
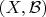
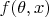
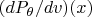
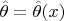
Let $(X,\mathcal{B})$ be a measurable space and $\{P_{\theta}, \ \theta \in \Theta\}$ a measurable family of laws on $(X,\mathcal{B})$, dominated by a $\sigma$-finite measure $v$. Let $f(\theta,x)$ be a jointly measurable version of the density $(dP_{\theta} /dv)(x)$ by Theorem 1.3.3. For each $x \in X$, a maximum likelihood estimate (MLE) of $\theta$ is any $\hat \theta= \hat \theta (x)$ such that $f(\hat \theta,x)=\sup\{f(\varphi, x): \varphi \in \Theta\}$. 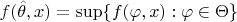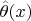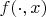In other words, $\hat \theta(x)$ is a point at which $f(\cdot,x)$ attains its maximum. In general, the supremum may not be attained, or it may be attained at more than one point. 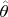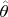If it is attained at a unique point $\hat \theta$,then $\hat \theta$ is called the maximum likelihood estimate of $\theta$. 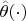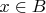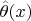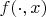A measurable function $\hat \theta(\cdot)$ defined on a measurable subset $B$ of $X$ is called a maximum likelihood estimator if for all $x \in B$, $\hat \theta(x)$ is a maximum likelihood estimate of $\theta$, and for $v$-almost all $x$ not in $B$, the supremum of $f(\cdot,x)$ is not attained at any point.

Ну т.е. главное, чтобы на каком-нибудь измеримом множестве иксов супремум на параметрическом множестве достигался, тогда на этом множестве полученная оценка и называется ОМП. Далее неоднократно подчеркивается, что супремум для каких-то иксов может в общем случае не достигаться, в том числе и для распределений экспоненциальных семейств.

3. Далее, в теореме про асимптотические свойства ОМП есть такое условие:

3.8 Efficiency of maximum likelihood estimators писал(а):

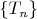
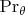
(EML-3) $\{T_n\}$ is a sequence of maximum likelihood estimators and is consistent, in other words $T_n \to \theta$ in $\mathrm{Pr}_\theta$-probability as $n \to \infty$ for all $\theta$.

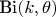
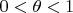
Здесь речь идет именно об ОМП, которая для $\text{Bi}(k,\theta)$ при $0 < \theta < 1$ не существует при $(0,...,0)$ и $(k,...,k)$, но существует для всех других иксов. Впрочем, это не страшно, так как вероятность попадания в эти два "особенных" случая стремится к нулю при $n \to \infty$ и на асимптотические свойства повлиять потому не может.