Итак, еще раз вернемся к рис.1.4:
и представим, каким образом СО'' должна была ускоряться начиная с нулевой скорости

по оси

при

по оси

:
Из начала координат движущейся с постоянной скоростью

по оси

ИСО стартует ракета, постоянно ускоряясь в направлении положительных значений оси

(см. рис. 1.5). В данном случае фронт разлета частиц (из начала координат изначально покоящейся СО') образует окружность, ракета стартует по касательной к фронту.
Далее (см. рис. 2.5, 3.5), по мере увеличения скорости

, скорость
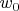
падает соответствуя

. Ускорение постоянно происходит по касательной к фронту разлета частиц с точкой начала движения в начале координат СО'. Рисунки выполнены без соблюдения масштаба ускорения, но принцип движения понятен. Очевидно, что при таком движении положение отвеса и показания уровня должны совпадать, а пробное тело в виде шарика останется лежать на дне «коробки». Вроде бы всё правильно, но такое представление влечет за собой некоторые сложности.
Представим, что точно такая же ракета стартует при нулевой скорости относительно АСО из начала координат, постоянно ускоряясь в направлении положительных значений оси

. Очевидно, что если где-то на оси

расположена точка финиша (в направлении движения ракеты), то рано или поздно ракета достигнет этой точки.
В рассмотренном выше случае, если подобная точка финиша расположена на оси

ИСО, движущейся относительно АСО по оси

с постоянной скоростью

, то при таком движении ракета не попадает в точку финиша, т.к. ее скорость
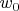
по мере ускорения падает, и ракета попросту «промахнется» мимо точки финиша, отклоняясь от оси

движущейся ИСО. На рис. 2.5 и 3.5 начало координат данной ИСО не отображено, т.к. по отношению к положению ракеты (СО''), начало координат данной ИСО находится далеко за обрезом рисунка на оси

.
Отсюда можно сделать вывод о том, что именно такое ускоренное движение как раз и позволяет обнаружить выделенную АСО, в которой ракета всегда попадает в точку финиша, расположенную по курсу движения стартовавшей ракеты. В общем случае, ракета стартовавшая из начала координат любой другой ИСО, при такой траектории движения должна промахиваться мимо точки финиша.
Таким образом, ускорение относительно мгновенно сопутствующей ИСО'' (отображенное на рис.1.4) невозможно экстраполировать на всю рассматриваемую траекторию, хотя именно такая траектория не позволяет обнаружить наличие абсолютного движения в «закрытой коробке».



