Можно просто исследованием на условный экстремум. Выходит долго, зато совершенно нехитро:
0) Очевидно, что если

или

то указанное выражение
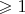
в дальнейшем будем считать, что
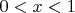
и
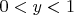
.
1) Исследуем на экстремум функцию

в квадрате
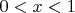
,
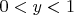
.
В точке минимума должны выполнятся равенства

Минимум должен лежать на кривой

2) Исследуем на экстремум функцию

В точке минимума должно выполнятся равенство


Случай

легко проверяется непосредственно (

), приравняв второй множитель к нулю и сделав соответствующие преобразования получим, что в точке минимума выполняется

3) Исследуем на экстремум функцию



при
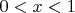
а поэтому если у функции

минимум на интервале
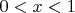
больше либо равен единице, то у функции

тем более.
В точке минимума должно выполнятся равенство



4) Исследуем на экстремум функцию

, мы хотим доказать, что

это тоже самое, что доказать

, поэтому исследуем функцию

В точке минимума должно выполнятся равенство



5) Исследуем на экстремум функцию

В точке минимума должно выполнятся



6) Функция

, очевидно

на интервале
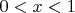
.
Что и завершает...



