Нужно посчитать интеграл.

Посчитал через

-функцию. Но, к сожалению, после замены

получил печальку -- в ответе вылез комплексный корень, так как при подстановке обратной функции под дифференциал

Далее интеграл распадается на два, в одном из которых в итоге появляется комплексный корень.
Собственно говоря, во втором случае трабла, когда
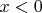
.
Также пробовал посчитать по общей формуле, но она слишком громоздкая, а при дифференцировании не дает верного ответа почему-то =( .
Я решал заменой, которую указал здесь.
Ответ, к сожалению, не помню. Все сдал ужо.
Но это не точно, говорю на память.



