Для нахождения сумм Гольдбаха вручную предлагается следующий алгоритм.
1. Для заданного четного числа

выписать суммы нечетных чисел равные

, начиная с суммы

и заканчивая суммой

.
2. Найти наибольшее нечетное число

, квадрат которого

меньше

.
3. Просматривать полученные суммы и зачеркивать те из них, в которых хотя бы одно из слагаемых кратно нечетным числам 3, 5, 7, 9, 11, 13, 15, ...

. Пропускать те значения

, которые кратны ранее использованному значению

,
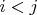
, например пропустить значения

=9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55 и т.д. Могут быть ошибочно зачеркнутые суммы:

, если число

простое,

, если число

простое и др.
4. Оставшиеся незачеркнутыми суммы есть представления числа

суммами двух простых чисел.
Например, для

значение

=7 и незачеркнутыми останутся суммы 13 + 47, 17 + 43, 19 + 41, 29 + 31, а сумма 7 + 31 зачеркнута ошибочно; для

значение

= 9 и незачеркнутыми останутся суммы 11 + 117, 17 + 101, 29 + 89, 47 + 71, 59 + 59, а сумма 5 + 113 зачеркнута ошибочно.
Примечания1. В системе Delphi алгоритм проверен до максимального числа

= 400000000, при этом первая незачеркнутая сумма 20129 + 399979871, ошибочно зачеркнуто 199 сумм (первые слагаемые незачеркнутых сумм 41, 53, 107, ..., 19319, 19553, 19739), Точное Количество представлений числа

суммами двух простых чисел равно

. Расхождение в процентах между

и количеством незачеркнутых сумм составляет 0.02\%, причем это расхождение с ростом

убывает.
2. Мне удалось доказать, что Минимальная Оценка Количества представлений четного числа

есть целая часть числа, равного корню квадратному из

, деленному на 4. Для чисел

= 60, 118, 1000, 1000000, 400000000 значения

равны, соответственно, 1, 2, 7, 250, 5000.