Внешний дифференциал

[svv]

Munin, вот бы Вы про цепи и коцепи рассказали, у Вас всегда такие хорошие объяснения получаются.

[Munin]

Думаю. Здесь либо трудоёмко, либо, возможно, не получится.

[Sicker]

попробуйте

[svv]

Sicker, у Вас получилось доказать, что если любой интеграл от формы равен нулю, то и форма равна нулю?

[Sicker]

ну это очевидно

[arseniiv]

А ещё вам очевидно, что такое самосознание…

[Sicker]

ага

[arseniiv]

Так что это даёт повод считать, что это не обязательно очевидно в среднем.

[svv]

Ладно, я тогда расскажу, как я сам себя в этом убеждаю.

Выберем точку $A$ в $M$, и в её касательном пространстве выберем $p$ линейно независимых векторов $\mathbf e_i,\;i=1..p$. Найдется $p$-мерное подмногообразие $D$, проходящее через $A$, к которому эти векторы будут касательными. В некоторой окрестности $A$ (в $D$) можно построить такую систему координат $u^i,\;i=1..p$, что векторы $\frac{\partial}{\partial u^i}$ координатного базиса в $A$ совпадут с $\mathbf e_i$. И пусть ещё все координаты $u^i$ равны нулю в точке $A$.

Возьмем «координатный параллелепипед» $P(\varepsilon)$ — множество точек той окрестности с координатами $0\leqslant u^i \leqslant \varepsilon$ (где $\varepsilon$ достаточно мало, чтобы точки с такими координатами нашлись). Тогда
$\int\limits_{P(\varepsilon)}\alpha=\alpha(\varepsilon\mathbf e_1, ..., \varepsilon\mathbf e_p)+o(\varepsilon^p)$
Левая часть равна нулю. Переходя к пределу при $\varepsilon\to 0$, получим
$\alpha(\mathbf e_1, ..., \mathbf e_p)=0$

[Munin]

Sicker
Между прочим, я вам вопрос задал, а ответа так и не дождался.

[Sicker]

да, знаю что такое тензоры
я по ним рк писал, в том семе

[Munin]

Чё такое рк?

-- 05.05.2014 03:10:14 --

Тогда, внешняя производная (Update: ранее было ошибочно написано "внешнее произведение") - это когда к тензору $T_{ij\ldots p}$ (нужным образом антисимметричному) приписывают ещё дифференцирование, и всё это опять антисимметризуют: $\partial_{[q}T_{ij\ldots p]}.$

Число компонент у такого тензора по мере ранга сначала растёт (когда ранг отдаляется от 0 к $n/2$), а потом уменьшается (когда ранг приближается от $n/2$ к $n$). Между двумя такими тензорами симметричных рангов $k$ и $n-k$ есть дуальность - дуальность Ходжа, или звёздочка Ходжа. 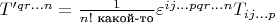Число независимых компонент у них одинаково, только расставлены они по-разному, и превратить один в другой можно символом Леви-Чивиты: $T'^{qr\ldots n}=\tfrac{1}{n!\text{ какой-то}}\varepsilon^{ij\ldots pqr\ldots n}T_{ij\ldots p}$ (нормировочного множителя я не помню и вспоминать не хочу; индексы, разумеется, потом снова спускаются вниз с небес на землю).

Поэтому, внешняя производная сначала делает из малокомпонентной штуки многокомпонентную, а потом постепенно - опять малокомпонентную.

В простейших случаях 1, 2 и 3 измерений операция внешней производной всем хорошо знакома:

$$f(x)\quad\xrightarrow{d}\quad\tfrac{d}{dx}f(x)$$

$$f(x,y)\quad\xrightarrow[\mathrm{grad}]{d}\quad(u,w)=(\tfrac{\partial}{\partial x}f,\tfrac{\partial}{\partial y}f)\quad\xrightarrow[\text{``}\mathrm{rot}\text{''}]{d}\quad\tfrac{\partial}{\partial x}w-\tfrac{\partial}{\partial y}u$$

$$f(x,y,z)\quad\xrightarrow[\mathrm{grad}]{d}\quad\vec{v}=\operatorname{grad}f\quad\xrightarrow[\mathrm{rot}]{d}\quad\vec{u}=\operatorname{rot}\vec{v}\quad\xrightarrow[\mathrm{div}]{d}\quad\rho=\operatorname{div}\vec{u}$$

-- 05.05.2014 03:16:50 --

При этом, видно, что применённая два раза, операция внешнего дифференцирования даёт тождественный ноль (это пишут как $dd=d^2=0$), но если форма была получена не внешней производной от другой формы, то тогда внешняя производная от неё имеет смысл, и может быть ненулевая.

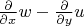
Выражение $\tfrac{\partial}{\partial x}w-\tfrac{\partial}{\partial y}u$ встречается в теореме Грина - аналог теоремы Стокса на плоскости. Если поменять местами компоненты вектора $(u',w')=(w,-u)$ (это означает поворот на 90°), то выражение станет $\tfrac{\partial}{\partial x}u'+\tfrac{\partial}{\partial y}w'=\operatorname{div}(u',w'),$ а теорема Грина - теоремой Гаусса.

[g______d]

Некоторый важный момент. Вообще говоря, производная тензора не является тензором. Нужно брать ковариантные производные, и результат зависит от метрики или связности. Но именно с внешней производной антисимметричного тензора такого не происходит; вся "нековариантность" сокращается.