Что такое дифференциал 2?

[yafkin]

Deggial: отделено от предыдущей темы в силу несоответствия ей.

А может начнем с начала? почему у товарища Зенона бегун не мог догнать черепаху?
и где же они встретятся?

[arseniiv]

1. Товарищ Зенон искусно использовал слова и отвлекал от того, что апория утверждала не совсем то. Две прямые с разными наклонами, очевидно, пересекаются.
2. Это не относится к теме. Зенон в понимании дифференциала не помощник, в его времена и понятия-то такого не было.

[nikvic]

yafkin в сообщении #853057 писал(а):

Это означает ,что значение настолько мало, что его невозможно записать цифрой
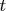
смысл имеет именно $ ds/dt $ - если$ s$ -расстояние, а $ t $ - время ,то$ \,\ v=ds/dt $
- это скорость

""бесконечно-малое - этта когда карамелька рассосалась, но сладость ощущаеца

Напрасно Вы думаете, что дифференциал - бесконечно-малая величина.

Классическое определение - главная линейная часть приращения некоей величины, а именно, той, имя которой пишется после буквы "d".
Подразумевается ситуация, когда несколько "величин" связаны гладкими функциями, и вблизи какой-то точки общего пространства эти зависимости заменяются линейными "наилучшим" образом.

[Brukvalub]

nikvic в сообщении #853856 писал(а):

...
Напрасно Вы думаете, что дифференциал - бесконечно-малая величина.

Классическое определение - главная линейная часть приращения некоей величины, а именно, той, имя которой пишется после буквы "d".
...

Это совсем уж неправильное "определение"!

[nikvic]

Brukvalub в сообщении #853860 писал(а):

Это совсем уж неправильное "определение"!

Интересно, Вы полагаете, что знаете правильное?

[Brukvalub]

nikvic в сообщении #853917 писал(а):

Brukvalub в сообщении #853860 писал(а):

Это совсем уж неправильное "определение"!

Интересно, Вы полагаете, что знаете правильное?

Даже не зная правильного определения, легко понять что "определение с главной линейной частью" не может быть правильным.

[yafkin]

На числовой оси берем точку $x_0$ создаем окрестность этой точки
содержащую $x$ $x\to x_0$-точке в которой считается
производная и где здесь $dx$?

[Brukvalub]

yafkin в сообщении #853925 писал(а):

На числовой оси берем точку $x_0$ создаем окрестность этой точки
содержащую $x$ $x\to x_0$-точке в которой считается
производная и где здесь $dx$?

Непосредственно перед вопросительным знаком в цитате.

[yafkin]

Аналогично поступая с $F(x)$ приходим к мысли ,что смысл имеет
только $F'(x)$

[Brukvalub]

yafkin в сообщении #853938 писал(а):

Аналогично поступая с $F(x)$ приходим к мысли ,что смысл имеет
только $F'(x)$

Имеет смысл не философствовать попусту на форуме, а почитать учебник.

[yafkin]

Далее следует по логике классическое определение дифференциала как главной части приращения

но все эти величины бесконечно малые и числом их не выразить вот так

-- 24.04.2014, 18:21 --

А учебник надо почитать тем участникам которые это определение старательно
запутывали

[Brukvalub]

Не понимаю я этих "хфилософов". Вот не знает или не понимает некто сто раз обкатанного со всех сторон в тысяче учебников понятия дифференциала, так возьми и прочти учебник, а потом выпиши его сюда со ссылкой на учебник и задай конкретный вопрос: "мне в этом определении непонятно то-то и то-то".
Так нет, вместо этого на пустом месте затевается нешуточный холивар на десяток страниц.

[yafkin]

-- 24.04.2014, 18:29 --

Вот Вам гопода учебник-все просто

[provincialka]

Какой-то корявенький учебник. Может, недаром не указан автор?

[ewert]

Это -- очень приблизительное определение. Собственно, оно с самого начала этого и не скрывает.