Рассмотрим задачу для некоторого (интегрально-)дифференциального оператора
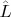
(

- область с гладкой границей

и всем, что необходимо

):

Под устойчивостью решения

(с соответствующими

и

) будем понимать

для достаточно малых

и

при разумно выбранной норме.
Понятно, что если оператор
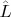
линеен, то устойчивость равносильна устойчивости на нулевом решении, то есть

для достаточно малых

и

.
При этом, кажется вполне понятном, что для нелинейного оператора
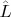
может существовать такая ситуация, когда решение

(с соответствующими

и

) устойчиво, а решение

(с соответствующими

и

) -- нет (поскольку непрерывность нелинейного оператора на каком-либо решении вовсе не равносильна его непрерывности в 0, как это было в случае линейного).
Не мог бы кто-нибудь из уважаемых членов сообщества подсказать простенькую задачу, для которой можно аналитически найти пару таких решений, или посоветовать, где можно посмотреть?



