Здравствуйте!
Я пишу небольшой доклад для конференции. Тема -- низкочастотная стабилизация верхнего положения равновесия маятника.
Сейчас все почти готово, но не получается сделать кое-какие выкладки. Подробнее:
Есть такое уравнение колебаний маятника с покоящейся точкой подвеса:

Перепишем его в другом виде:

(в предположении, что трение пропорционально скорости), где

-- угол отклонения, отсчитываемый от нижнего положения равновесия,

-- коэффициент трения подшипника в точке подвеса,

-- собственная частота малых колебаний (

-- длина маятника,

-- ускорение свободного падения).
Пусть точка подвеса совершает колебания в вертикальном направлении по закону

, где

-- некоторая периодическая функция. Чтобы составить уравнение колебаний маятника с вибрирующей точкой подвеса воспользуемся принципом относительности, согласно которому движение маятника с вертикально вибрирующей точкой подвеса эквивалентно движению маятника с покоящейся точкой подвеса, находящемуся в поле <<силы тяжести>> с ускорением

. Поэтому заменим в (1)

на

. Это возможно, так как мы просто переходим к новой системе отсчета в физической модели. В результате получим искомое уравнение:

Уравнение (2) допускает стационарное решение

, соответствующее верхнему положению равновесия маятника (стационарное решение

соответствует нижнему положению равновесия маятника).
Проведем линеаризацию данного уравнения маятника. Для этого разложим функцию

в ряд Тейлора, после чего оставим в разложении только линейные члены относительно

. Из формулы разложения функции в ряд Тейлора в заданной точке

(где

) имеем:


Отсюда:

Тогда уравнение первого приближения (уравнение в вариациях) выглядит так:

где

-- ускорение точки подвеса,

-- собственная частота малых колебаний.
Исследуем уравнение (3). Задача состоит в том, чтобы найти функцию

такую, чтобы положение равновесия уравнения (3), когда

,

(то есть, когда угол отклонения равен нулю и скорость равна нулю) было асимптотически устойчивым.
Перейдем от уравнения (3) к эквивалентной ему системе (

,

)

где стабилизирующая функция

подлежит определению.
Будем искать стабилизирующую функцию

в классе кусочно-постоянных периодических с периодом

(где

-- достаточно большое число) функций вида

(где

), имеющих нулевое среднее на периоде.
Для функций

вида (5) покажем возможность стабилизации верхнего положения равновесия маятника при низкочастотных колебаниях точки подвеса. Для этого мы рассмотрим поведение системы (3) отдельно во всех трех случаях значения стабилизирующей функции

.
Имеет место следующая теорема.
Теорема. Пусть в системе (4), (5)

Тогда для любого числа  существует число
существует число  такое, что система (4) с функцией
такое, что система (4) с функцией  вида (5) асимптотически устойчива.Доказательство.
вида (5) асимптотически устойчива.Доказательство. Прежде всего, заметим, что, не умаляя общности, можно считать

Этого можно добиться всегда, сделав в уравнении (3) или в системе (4) замену времени
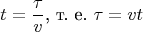 Вот это именно то место, в котором у меня возникают проблемы.
Вот это именно то место, в котором у меня возникают проблемы.Проведем некоторые выкладки:


Подставим эти результаты в уравнение (3):
Пусть

:



Преподаватель говорил, что

-- это частота, поэтому ее можно принять за единицу. Тогда:

Но то, что посерединке, никак не похоже на то, что должно быть в (7), и я даже не представляю, можно ли к этому как-нибудь прийти.
Пожалуйста, подскажите, как выпутаться из этой проблемы.
Большое спасибо за помощь!



