Я полагал, что для расчета эволюции надо...
Покажу на примере трёхмерного УКГ

Уравнение второго порядка по времени, значит при

надо задать значения поля и значения его первой производной по времени. Начальные условия:

Тогда в произвольный момент времени

поле

можно вычислить по формуле:

Чтобы выполнялось (2) пропагаторы

и

должны удовлетворять следующим начальным условиям:


Решая уравнение (1) с начальными условиями (4) и (5) получаем ответ:


Интегралы (6) и (7) не сходятся, то есть величины

и

не являются числовыми функциями, а являются лишь абстрактными символами обозначающими правую часть (6) и (7). Использовать символы

и

можно лишь подставив их в формулу (3) и поменяв порядок интегрирования: сначала взять интеграл по

, затем по

.
До некоторой степени с символами

и

можно обращаться как с обычными функциями, вот только их графиков нельзя построить, так как числовых значений они не имеют.
Для рассмотрения сферически симметричного случая можно перейти в (6) и (7) к сферической системе координат в импульсном пространстве:


Рассмотрим эволюцию гауссовского волнового пакета

Подставляя символ (6') в формулу (3), меняя порядок интегрирования и беря интеграл по

получаем ответ:

При интегрировании по

я перешёл в сферическую систему координат

и воспользовался формулой

.
Всё, ответ (9) можно рисовать:

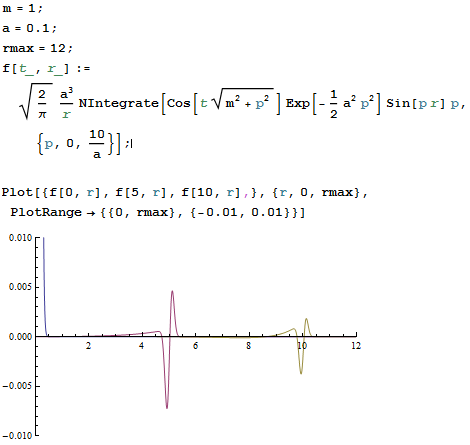

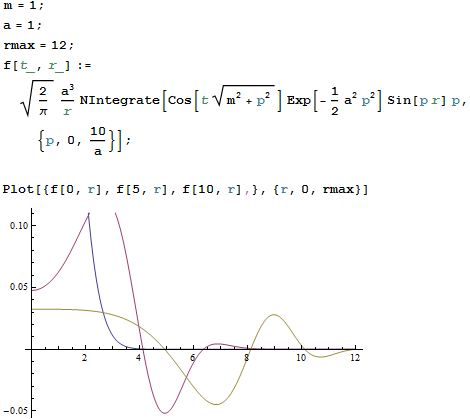
Попытка заменить
несходящиеся интегралы (символы)

и

функциями Бесселя приведёт к плачевному результату,
зря мы с вами потратили время на рисование функций Бесселя.