Теорема Паули по учебнику авторства Кушниренко

[Name XXX]

В учебнике авторства А.Н. Кушниренко (издательства 1983 года; год издания важен, так как в предыдущем издании обсуждаемый материал отсутствует) приведено доказательство теоремы Паули о связи спина со статистикой. Доказательство мне кажется чрезмерно феноменологическим. Возможно, впрочем, что я просто не понимаю часть аргументов. Потому и решил задать вопрос про это.

Ниже я приведу эти спорные аргументы. Перед этим придется также в информативных целях привести и все доказательство в тезисном виде, так как издание указанного выше года в свободном доступе (в электронном виде) я не нашел. Спорные моменты будут выделены курсивом, а в конце поста будут приведены причины, по которым я считаю их спорными. По просьбе могу прикрепить фотографии страниц с доказательством.

1. Автор показывает, что для случая свободных скалярного, электромагнитного и дираковского полей для разных моментов времени перестановочные соотношения $[\Psi (x), \Psi^{\dagger} (x')]_{\pm}$ выражаются через функцию $D_{0} (x - x')$, которая имеет вид

$$ D_{0}(x - x') = \int e^{i(\mathbf p \cdot (\mathbf x - \mathbf x'))}\frac{sin(\epsilon_{\mathbf p}(t - t')}{\epsilon_{\mathbf p}}\frac{d^{3}\mathbf p}{(2 \pi)^{3}}, \quad \epsilon_{\mathbf p}^{2} = \mathbf p^{2} + m^{2}. $$

Здесь интегрирование ведется по всему импульсному пространству.
Например, для случая дираковского поля антикоммутатор дает

$$ [\Psi (x), \Psi^{\dagger} (x')]_{+} = (i\gamma^{\mu}\partial_{\mu} + m)D_{0}(x - x'). $$

2. Далее автор говорит, что для релятивистски-инвариантной локальной квантовой теории поля должно выполняться следующее: если точки $x, x'$ в пространстве Минковского разделены пространственноподобным интервалом, то измерение некоторой физической величины в точке $x$ не повлияет на измерение этой величины в точке $x'$. На формальном языке квантовой механики это означает, что для соответствующего оператора $\hat {L}(x)$ должно выполняться равенство

$$ [\hat {L}(x), \hat {L}(x')] = 0, \quad x^{2} < 0 . \qquad (1) $$

3. Далее автор сужает класс операторов $\hat {L}$ до таких, которые есть билинейными формами от физических полей. Действительно, основные физические операторы для скалярного, фермионного и электромагнитного полей именно таковыми и являются, и автор обобщает это на случай произвольных спинов. При таком условии равенство $(1)$ означает, что поля должны подчиняться одному из соотношений

$$ [\Psi (x), \Psi^{\dagger}(x')]_{\pm} = G_{ab}^{\pm}(x - x'), $$

где $G_{ab}^{pm}(x - x')$ - некоторая неоператорная функция, которая обращается в нуль на пространственноподобном интервале.
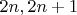4. Далее автор утверждает, что если $\psi_{a}$ - компоненты функции, описывающей частицу с некоторым произвольными спином, то $\psi_{a}\psi_{b}$ - тензор ранга $2n, 2n + 1$ для частиц со спином $n, n + \frac{1}{2}$ соответственно [1]. После чего утверждает, что, согласно п. 1, тензоры $G_{ab}^{\pm}(x - x')$ выражаются через функцию $D_{0}(x - x')$ как [2]

$$ G_{ab}^{\pm}(x - x') = F_{ab}^{(h)}\left( \frac{\partial}{\partial x}\right)D_{0}(x - x'), $$

где $F_{ab}^{(h)}\left( \frac{\partial}{\partial x}\right)$ - некоторый полином по производным степени $h$, а $h$, в свою очередь, равно $h = 2n, 2n + 1$ и соответствует спину частицы.
5. Далее автор исходя из требования положительности энергии и условия положительности метрики $\langle \Psi | \hat {A}^{+} \hat {A} | \Psi \rangle > 0$ [3] получает правила коммутации и антикоммутации для полей соответствующих спинов.


А вот, собственно, то, что кажется мне непонятным в выделенных тезисах.

1. В каком смысле величина $\psi_{a}\psi_{b}$ есть тензором? Относительно чего она есть тензором? В пространстве каких индексов (векторных, спинорных)? Тот же дираковский спинор, который есть прямой суммой представлений $\left(\frac{1}{2}, 0\right) \oplus \left(0, \frac{1}{2}\right)$ группы Лоренца, не дает 4-вектор (то есть, 4-тензор нечетного ранга 1) сверткой $\Psi_{a}(x)\Psi_{b}(x')$. Тогда мне непонятно, с чего бы полуцелый спин соответствовал тензору нечетного ранга.

2. Это утверждение мне также непонятно. Как можно так просто обобщить результаты для спинов $0, 1, \frac{1}{2}$ на случай произвольного спина? Понимаю, уравнения, которые описывают поля целых и полуцелых спинов, формально похожи друг на друга (например, поле целого спина $n$ соответствует симметричному бесследовому и поперечному по всем индексам (в смысле $\partial_{\mu_{i}}F^{\mu_{1}...\mu_{i}...\mu_{n}} = 0$ для всех $i$) тензору, который удовлетворяет уравнению Клейна-Гордона, и это все очень похоже на случай электромагнитного поля. Однако все равно это обобщение как-то слишком уж притянуто за уши, на мой взгляд.

3. Тоже непонятно. Уже для случая скалярного поля метрика не есть положительно определенной, ведь лоренц-инвариантная норма дается выражением $\int j_{0}d^{3}\mathbf r$, которое не всегда больше нуля. Что именно имел в виду автор?

Помогите, если знаете ответ. Я сильно страдаю и не могу разобраться с этим уже довольно много времени.

[espe]

Name XXX в сообщении #840419 писал(а):

3. Тоже непонятно. Уже для случая скалярного поля метрика не есть положительно определенной, ведь лоренц-инвариантная норма дается выражением $\int j_{0}d^{3}\mathbf r$, которое не всегда больше нуля. Что именно имел в виду автор?

Вы здесь путаете РКМ (релятивистскую квантовую механику) с КТП (квантовой теорие поля). В КТП скалярное произведение определяется не так.

Name XXX в сообщении #840419 писал(а):

если $\psi_{a}$ - компоненты функции, описывающей частицу с некоторым произвольными спином, то $\psi_{a}\psi_{b}$ - тензор ранга $2n, 2n + 1$ для частиц со спином $n, n + \frac{1}{2}$ соответственно [1].

Может быть там написано что-то типа $\psi_{a}\psi_{b}^+$? (Один из сомножителей имхо должен быть сопряжённый.)

Name XXX в сообщении #840419 писал(а):

По просьбе могу прикрепить фотографии страниц с доказательством.

Выложите если не трудно. Но не обещаю, что что-то смогу ответить.

[Name XXX]

По поводу первого - спасибо, я сглупил. Тут же на фоковском пространстве определено произведение.

По поводу второго - все равно ведь можно подобрать такие компоненты $a, b$, чтобы величина соответствующей спинорной функции $\psi_{a} \psi^{\dagger}_{b}$ не соответствовала тензору нечетного ранга.

Фотографии выложу чуть позже.

[espe]

Name XXX в сообщении #841014 писал(а):

По поводу второго - все равно ведь можно подобрать такие компоненты $a, b$, чтобы величина соответствующей спинорной функции $\psi_{a} \psi^{\dagger}_{b}$ не соответствовала тензору нечетного ранга.

Любое поле можно с помощью сигма-матриц записать как спин-тензорное поле $\psi_{a_1\cdots a_n\dot{b}_1\cdots\dot{b}_m},$ $a,\dot{b}=1,2$. Спин такого поля $s=(m+n)/2.$ При комплексном сопряжении точечные (пунктирные) индексы становятся не точечными и наоборот и комбинация $\psi\psi^*$ будет содержать одинаковое количество точечных и неточечных индексов и такой объект с помощью сигма-матриц можно преобразовать в тензорное поле спина (ранга) $2s$ (с пространственно-временными индексами).

[Name XXX]

Согласен с Вашим утверждением, однако, все же, уточню его (прокомментируйте, пожалуйста, правильно ли я понял его), дабы в будущем избежать недоразумений в связи с ним.

Возьмем представление (для простоты) дираковских спиноров. Ваше утверждение значит, что если рассмотреть прямое произведение этих представлений,

$$ \left(\left( \frac{1}{2}, 0 \right) \oplus \left( 0, \frac{1}{2} \right) \right) \otimes \left(\left( \frac{1}{2}, 0 \right) \oplus \left( 0, \frac{1}{2} \right) \right) = $$

$$ = \left(0 , 0 \right) \oplus \left( 1, 0 \right) \oplus \left( \frac{1}{2}, \frac{1}{2} \right) \oplus \left( \frac{1}{2}, \frac{1}{2} \right) \oplus \left( 0 , 1 \right) \oplus \left(0, 0 \right), $$

то представления вида $\left( 1, 0 \right) \Rightarrow \Psi_{a b}$ можно преобразовать оператором $\Delta_{\dot {a}}^{\quad a} = \frac{1}{m}(\sigma_{\mu})_{\dot {a}}^{\quad a}\partial^{\mu}$ в представление $\left( \frac{1}{2}, \frac{1}{2}\right)$, которое все так же будет удовлетворять условиям неприводимости по группе Пуанкаре. И тогда все неприводимые представления будут соответствовать тензору ранга 1.
Аналогичное утверждение справедливо для любого представления данного спина.

Так?

Кстати, если мы берем прямую сумму представлений $(m, n) \oplus (n, m)$ (чтобы оно было инвариантно относительно полной группы Лоренца), то утверждение автора про то, что $\psi_{a}\psi_{b}$, является тензором, верно в любом случае. Автор всегда берет прямую сумму представлений полуцелого спина (это видно из фотографии 3 ниже).


-- 26.03.2014, 22:09 --

Ссылки на фотографии раздела с доказательством приведены ниже. В них $D_{m}$ - пропагатор, что у меня обозначен как $D_{0}$.

(Оффтоп)

,

,
.

[espe]

Name XXX в сообщении #841280 писал(а):

представления вида $\left( 1, 0 \right) \Rightarrow \Psi_{a b}$ можно преобразовать оператором $\Delta_{\dot {a}}^{\quad a} = \frac{1}{m}(\sigma_{\mu})_{\dot {a}}^{\quad a}\partial^{\mu}$ в представление $\left( \frac{1}{2}, \frac{1}{2}\right)$,

Я думаю, что так, ведь $\psi$ удовлетворяет уравнениям движения.

[Name XXX]

espe, а что Вы думаете по поводу неясного момента из пункта 2?
У меня сейчас такое феноменологическое предположение: "пропорциональность" коммутатора функции $D_{0}$ есть выражением того факта, что:
1. Эта функция является релятивистски инвариантной и удовлетворяет равенству нулю для любого пространственноподобного интервала.
2. Уравнения для поля любого целого спина являются однотипными по своему виду. То же самое - для поля полуцелого спина.
3. Все это значит, что (анти-)коммутатор полей любого спина имеет общую структуру некоторого оператора, который действует на функцию $D_{0}$. Вид оператора определяется уже размерностью представления.

Правда, отсюда никак не следует, с чего бы тот оператор является полиномом по производным.

[espe]

Думаю, что примерно так. Оператор поля $\psi_A$ (удовлетворяющий уравнениям движения) имеет структуру

$$\psi_A(x)\sim\int d^3p\,\Bigl\{e^{\ldots}\;a_A(p)+e^{\ldots}\;\bar{b}_A(p)\Bigr\}\,,$$

$a_A$ и $\bar{b}_A$ -- операторы рождения и уничтожения и все сведения о спине поля содержаться в них, экспоненты будут одинаковыми для полей всех спинов (обычное разложение Фурье). Сопряженное поле будет выглядеть примерно так

$$\bar{\psi}_{A'}(x)\sim\int d^3p\,\Bigl\{e^{\ldots}\;\bar{a}_{A'}(p)+e^{\ldots}\;b_{A'}(p)\Bigr\}\,.$$

Коммутаторы операторов рождения и уничтожения $\sim F_{AB}\delta(p-p'),$ $F_{AB}$ от $p$ не зависит и опять вся информация о спине поля содержится в $F$. Теперь смотрим на коммутатор полей. Он будет (скорее всего сумма по таким объектам или подобных объектов) $\sim F_{AB}D_0(x-x').$ Здесь опять $D_0$ будет общая для всех спинов, т.к. она возникает из интегралов по $p$ и $p'$, экспонент и дельта-функции (которые для всех спинов одинаковые). Теперь разбираемся с $F_{AB}$. Если в нём одинаковое количество точечных и неточечных индексов, то с помощью сигма-матриц делаем из него тензор (в смысле с пространственно-временными индексами). Если количество точечных и неточечных индексов разное, то несколько раз преобразуем

Name XXX в сообщении #841280 писал(а):

оператором $\Delta_{\dot {a}}^{\quad a} = \frac{1}{m}(\sigma_{\mu})_{\dot {a}}^{\quad a}\partial^{\mu}$ в представление

в котором количество точечных и неточечных индексов совпадает. Отсюда и появляются производные действующие на $D_0$. В самом «худшем» случае, когда у $F_{AB}$ все индексы одного типа такое преобразование нужно будет сделать $2s$ раз и появятся $2s$ производные действующие на $D_0$.

Думаю, что для стандартных реализаций, когда для бозонов используются тензорные поля производных вообще не будет и для фермионов, когда используются спиноры с $s-1/2$ тензорными индексами будет только одна производная.

[Name XXX]

espe, спасибо!
Я с Вами практически полностью согласен. Только немного сомневаюсь насчет того, что для (анти-)коммутаторов операторов рождения-уничтожения и полей функция $F_{ab}$ будет одной и той же (даже с учетом суммы). Ведь для перестановочных соотношений на операторы рождения-уничтожения не может возникнуть производная, так как они не зависят от координат.

[espe]

Name XXX в сообщении #842443 писал(а):

Ведь для перестановочных соотношений на операторы рождения-уничтожения не может возникнуть производная

Если $F_{AB}$ не зависит от $p$, то производные не возникают. Я об этом написал

espe в сообщении #842187 писал(а):

$F_{AB}$ от $p$ не зависит

-- Сб мар 29, 2014 08:20:48 --

Name XXX в сообщении #842443 писал(а):

Только немного сомневаюсь насчет того, что для (анти-)коммутаторов операторов рождения-уничтожения и полей функция $F_{ab}$ будет одной и той же

$$[\psi_A(x),\bar{\psi}_{A'}(x')]\sim\int d^3p\int d^3p'\Bigl\{e^{if(p,p',x,x')}[a_A,\bar{a}_{A'}]+\ldots\Bigr\}=$$

$$=\int d^3p\int d^3p'\Bigl\{e^{if(p,p',x,x')}F_{AA'}\delta(p-p')+\ldots\Bigr\}=F_{AA'}D_0(x,x')+\ldots$$

Вроде бы так

[Name XXX]

Но $F_{ab}$ в общем случае зависит от $p$. Например, для биспиноров $\hat {A} = \hat {a}_{s}(\mathbf p )u_{s}(\mathbf p)$, и тогда (сумма по поляризациям взята для удобства)

$$ \sum_{s}[\hat {A}_{s}(\mathbf k ), \hat {A}^{\dagger}_{s'}(\mathbf p)]_{+} = \sum_{s}u_{s}\bar {u}_{s}\gamma_{0} = (\gamma^{\mu}p_{\mu} + m)\gamma_{0}. $$

В результате, это выражение нельзя выносить за знак интеграла $D_{0}$. Чтобы можно было, нужно вначале записать что-то вроде $\gamma^{\mu}pe^{-ipx} = i\gamma^{\mu}\partial_{\mu}e^{-ipx}$, и тогда можно будет выделить функцию $D_{0}$.

[espe]

Да, пропустил я зависимость от $p,$ да и вообще преобразования с $\Delta$ здесь не причём.

У меня сложилось впечатление, что у Кушниренко бозонные поля -- это тензорные поля ранга $s,$ а фермионные -- спиноры с $s-1/2$ тензорными индексами.

Очередной вариант объяснения.
Пусть индекс $A$ -- это $n$ тензорных индексов, у фермионов ещё подразумевается наличие дираковского индекса. Итак имеем

$$[\psi_A(x),\bar{\psi}_{A'}(x')]\sim\int d^3p\int d^3p'\Bigl\{e^{\pm ipx\pm ip'x'}F_{AA'}(p)\delta(p-p')+\ldots\Bigr\}=\int d^3p\Bigl\{e^{\pm ip(x\pm x')}F_{AA'}(p)+\ldots\Bigr\}$$

$F_{AA'}$ -- это тензор ранга $2n$ зависящий от $p$. Его можно составить из $p_\mu$ и метрики. Количество $p_\mu$ четное и максимальная степень $p_\mu$ равна $2n$. Следовательно у бозонов максимальная степень производных $2n$ и количество производных чётное. У фермионов есть ещё два дираковских индекса и возможный вариант -- как у спина 1/2.

[Name XXX]

Для бозонных полей Ваш ответ прозрачен. В самом деле, операторы $\Delta $ не нужны (по крайней мере, я уверен в этом утверждении для случая бозонов). Однако мне не совсем ясно, что делать с фермионным случаем. Для удобства снова можно воспользоваться случаем уравнения Дирака:

$$ [\hat {\Psi}_{a}(x), \hat {\bar {\Psi}}_{b}(x')]_{+} = \left(i\gamma^{\mu}\partial_{\mu} + m\right)_{ab}D_{0}(x - x'). $$

Тут возникает такой вопрос. Если рассмотреть отдельные блочные части матрицы $i\gamma^{\mu}\partial_{\mu} + m$ (разложить, короче, в прямую сумму неприводимых представлений), то будет видно, что часть из них действительно соответствует представлению 4-вектора, а другая же часть соответствует представлению $(0, 0)$. Это все значит, что можно выбрать такие $a, b$ (тут каждый из $a, b$ помечает один из спиноров, образующий дираковский спинор $\Psi = \begin{pmatrix} \varphi_{a} & \kappa^{\dot {a}}\end{pmatrix}$), что не будет давать производной. Это значит, что и в общем случае биспинора

$$ \Psi_{\mu_{1}...\mu_{n}} = \begin{pmatrix} \varphi_{a, \mu_{1}...\mu_{n}}\\ \kappa^{\dot {a}}_{\quad \mu_{1}...\mu_{n}}\end{pmatrix} \equiv \left( \frac{n + 1}{2}, \frac{n}{2}\right) \oplus \left( \frac{n}{2}, \frac{n + 1}{2}\right), $$

который задает представление $n +\frac{1}{2}$ (Кушниренко пользуется, вроде, таким представлением, что косвенно подтверждается размерностью матрицы $\Gamma^{\mu}$ уравнения (3.7.7) док-ва), тоже можно будет выбрать такие компоненты, где спинорная часть не будет давать еще одну производную. А это значит, что в антикоммутаторе для таких полей будут также производные лишь четного порядка, что противоречит заявлению Кушниренко, который утверждает, что будут содержаться лишь производные нечетного порядка. Как это учесть?

[espe]

Для фермионов я тоже не понимаю почему только нечётные степени производных. Для спина 1/2 можно вычислить в лоб

Name XXX в сообщении #844317 писал(а):

$$[\hat {\Psi}_{a}(x), \hat {\bar {\Psi}}_{b}(x')]_{+} = \left(i\gamma^{\mu}\partial_{\mu} + m\right)_{ab}D_{0}(x - x').$$

Видно, что здесь есть слагаемое с массой без производных и какие преобразования надо сделать, чтобы осталаись только первые степени производных (избавиться от слагаемого с массой) я не вижу.

[Name XXX]

espe, кажется, я понял, что имелось в виду. Автор стартует с определения функции произвольного спина как такой, что целому спину n сопоставляет тензор ранга n, полуцелому спину $n + \frac{1}{2}$ - объект с одним спинорным индексом и n векторными. Тогда понятно, что в выражении $[\Psi_{a}(x), \hat {\Psi}_{b}^{\dagger}(y)]_{\pm}$ будут два тензора ранга $2s$.
Но непонятно вот что. Именно, для

$$ \hat {\Psi}_{a}(x) = \sum_{\sigma}\int \frac{d^{3}\mathbf p}{\sqrt{(2 \pi)^{3}2 \epsilon_{\mathbf p}}}\left(A^{\sigma}_{a}(\mathbf p) \hat {a}^{\sigma} (\mathbf p)e^{-ipx} + B^{\sigma}_{a}(\mathbf p) \hat {{b}^{\sigma}}^{\dagger} (\mathbf p)e^{ipx}\right) $$

можно получить нечто вроде

$$ [\Psi_{a}(x), \hat {\Psi}_{b}^{\dagger}(y)]_{\pm} = \sum_{\sigma}\int \frac{d^{3}\mathbf p}{(2 \pi)^{3}2 \epsilon_{\mathbf p}}\left(A^{\sigma}_{a}(\mathbf p){A^{\sigma}}^{\dagger}_{b}(\mathbf p) e^{-ip(x - y)} \pm B^{\sigma}_{a}{B^{\sigma}}^{\dagger}_{b}(\mathbf p) e^{ip(y -x)}\right). $$

Непонятно, на основе чего автор так просто заключает, что функция $A^{\sigma}_{a}(\mathbf p)$ тесно связана с $B^{\sigma {'}}_{a}(\mathbf p)$. Он, конечно, мог это постулировать, однако в этой связи есть куча подводных камней, в результате чего часть формулировки теоремы Паули про положительность энергии просто не нужна.