Найти СЛАУ задающую линейное подпространство, натянутое на следующую систему векторов:

Получается нужно написать СЛАУ по её фундаментальной системе решений, в данном случае эта система, выглядит так:

Получается что СЛАУ состоит из двух уравнений c 4 неизвестными
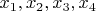
Как мне теперь найти коэффициенты перед этими неизвестными?
Я составил такую вот СЛАУ:

Теперь по идее если её решить, получим новую ФСР, если из неё взять 2 линейно независимых решения, это и будут коэффициенты. Я на верном пути или нет?
-- 18.03.2014, 18:58 --Всё, вопрос снят, всем спасибо.



