Вообще, хоть она тут и названа
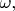
но логичней её назвать

Эта константа - волновое число (модуль волнового вектора) для искомой стоячей волны, то есть

- обратная длина волны.
Разумеется, она может принимать какое угодно значение, и малое, и большое. Но по сути, для математики видно, что эта величина размерная: она имеет размерность

и изменением масштаба единиц измерения длины уравнение всегда может быть приведено к виду

Просто от этого изменятся масштабы той области, в которой ищется решение: она увеличится или уменьшится, чтобы сохранить своё соотношение с длиной волны.



