Нарисовал картинки. Увидел, что белая дыра Пэнлеве и чёрная дыра Пэнлеве отделены друг от друга бесконечностью по времени Пэнлеве.
Чёрная дыра ПэнлевеИсходная метрика:

В изотропных координатах:



В координатах традиционной ориентации:



Картинка:
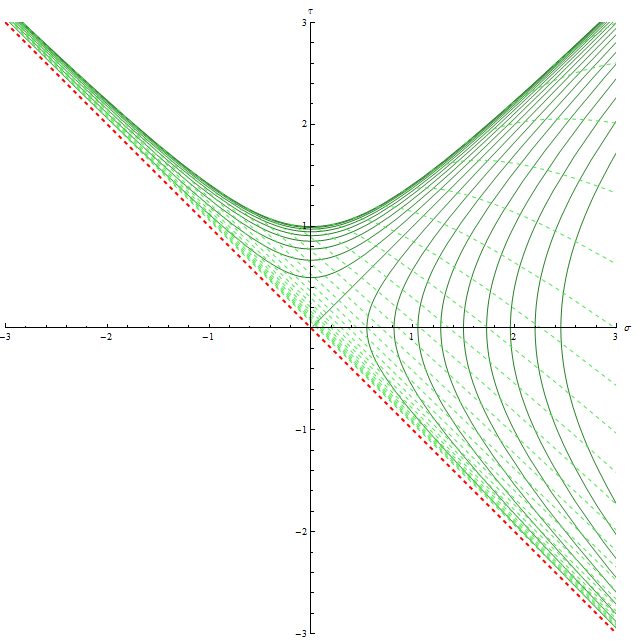
Сплошные линии: поверхности

Пунктирные линии: поверхности

Красная пунктирная левая диагональ: бесконечно далёкое прошлое

Сплошная правая диагональ:
 Белая дыра Пэнлеве
Белая дыра ПэнлевеИсходная метрика:

В изотропных координатах:



В координатах традиционной ориентации:



Картинка:
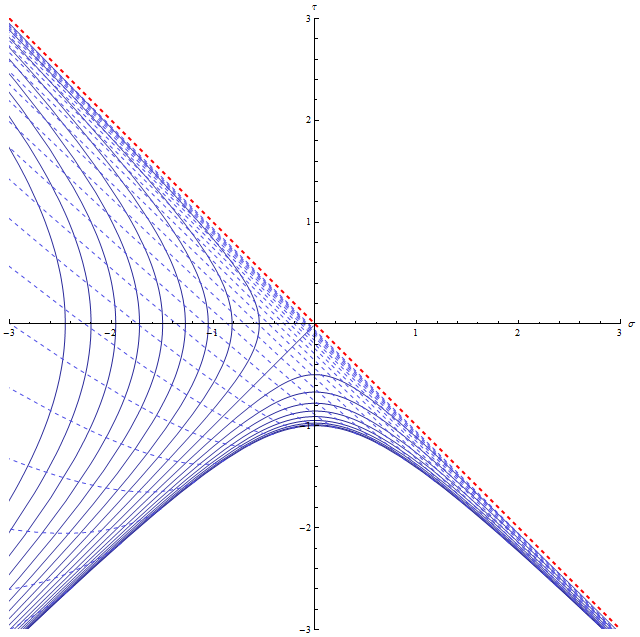
Сплошные линии: поверхности

Пунктирные линии: поверхности

Красная пунктирная левая диагональ: бесконечно далёкое будущее

Сплошная правая диагональ:
 Белая и чёрная дыра Пэнлеве вместе
Белая и чёрная дыра Пэнлеве вместе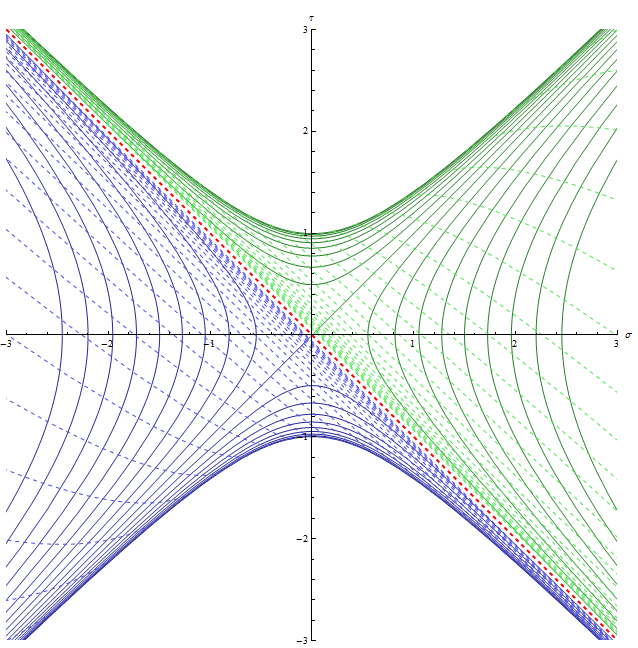
Сплошные линии: поверхности

Пунктирные линии: поверхности

Красная пунктирная левая диагональ: бесконечно далёкое будущее

для вселенной белой дыры Пэнлеве
и, одновременно, бесконечно далёкое прошлое

для вселенной чёрной дыры Пэнлеве.
Сплошная правая диагональ:
 Белая дыра Пэнлеве и чёрная дыра Пэнлеве отделены друг от друга бесконечностью по времени Пэнлеве.
Белая дыра Пэнлеве и чёрная дыра Пэнлеве отделены друг от друга бесконечностью по времени Пэнлеве.(Программа на Mathematica)
L = 7;
W = 3;
dT = 0.4;
NT = 15;
dR = 0.1;
NR = 9;
range = {{-W, W}, {-W, W}};
(* Чёрная дыра Пэнлеве *)
Clear[c, rg, r, t, dt, dr, \[Xi], \[Chi], \[Tau], \[Sigma]];
\[Xi][t_, r_] :=
Exp[(-c t + r + 2 Sqrt[rg r])/(2 rg)] (1 - Sqrt[r/rg]);
\[Chi][t_, r_] :=
Exp[(+c t + r - 2 Sqrt[rg r])/(2 rg)] (1 + Sqrt[r/rg]);
d\[Xi] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Xi][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Xi][t, r]\)\) dr;
d\[Chi] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Chi][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Chi][t, r]\)\) dr;
Simplify[(4 rg^3)/r E^(-(r/rg))
d\[Xi] d\[Chi] == (c^2 dt^2 - (dr + Sqrt[rg/r] c dt)^2), {r > 0,
rg > 0}]
\[Tau][t_, r_] := 1/2 (\[Xi][t, r] + \[Chi][t, r]);
\[Sigma][t_, r_] := 1/2 (\[Chi][t, r] - \[Xi][t, r]);
d\[Tau] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Tau][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Tau][t, r]\)\) dr;
d\[Sigma] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Sigma][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Sigma][t, r]\)\) dr;
Simplify[(4 rg^3)/
r E^(-(r/
rg)) (d\[Tau]^2 -
d\[Sigma]^2) == (c^2 dt^2 - (dr + Sqrt[rg/r] c dt)^2), {r > 0,
rg > 0}]
c = 1;
rg = 1;
radial[r_] :=
ParametricPlot[{\[Sigma][t, r], \[Tau][t, r]}, {t, -L, L},
PlotRange -> range, PlotStyle -> {RGBColor[0.15, 0.5, 0.15]}];
time[t_] :=
ParametricPlot[{\[Sigma][t, r], \[Tau][t, r]}, {r, -L, L},
PlotRange -> range, PlotStyle -> {RGBColor[0.3, 0.9, 0.3], Dashed}];
blackRadial = Table[radial[1 + n*dR], {n, -NR, NR}];
blackTime = Table[time[n*dT], {n, -NT, NT}];
black = Join[blackRadial, blackTime];
(* Белая дыра Пэнлеве *)
Clear[c, rg, r, t, dt, dr, \[Xi], \[Chi], \[Tau], \[Sigma]];
\[Xi][t_,
r_] := -Exp[(+c t + r + 2 Sqrt[rg r])/(2 rg)] (1 - Sqrt[r/rg]);
\[Chi][t_,
r_] := -Exp[(-c t + r - 2 Sqrt[rg r])/(2 rg)] (1 + Sqrt[r/rg]);
d\[Xi] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Xi][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Xi][t, r]\)\) dr;
d\[Chi] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Chi][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Chi][t, r]\)\) dr;
Simplify[(4 rg^3)/r E^(-(r/rg))
d\[Xi] d\[Chi] == (c^2 dt^2 - (dr - Sqrt[rg/r] c dt)^2), {r > 0,
rg > 0}]
\[Tau][t_, r_] := 1/2 (\[Xi][t, r] + \[Chi][t, r]);
\[Sigma][t_, r_] := 1/2 (\[Chi][t, r] - \[Xi][t, r]);
d\[Tau] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Tau][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Tau][t, r]\)\) dr;
d\[Sigma] = \!\(
\*SubscriptBox[\(\[PartialD]\), \(t\)]\(\[Sigma][t, r]\)\) dt + \!\(
\*SubscriptBox[\(\[PartialD]\), \(r\)]\(\[Sigma][t, r]\)\) dr;
Simplify[(4 rg^3)/
r E^(-(r/
rg)) (d\[Tau]^2 -
d\[Sigma]^2) == (c^2 dt^2 - (dr - Sqrt[rg/r] c dt)^2), {r > 0,
rg > 0}]
c = 1;
rg = 1;
radial[r_] :=
ParametricPlot[{\[Sigma][t, r], \[Tau][t, r]}, {t, -L, L},
PlotRange -> range, PlotStyle -> {RGBColor[0.15, 0.15, 0.6]}];
time[t_] :=
ParametricPlot[{\[Sigma][t, r], \[Tau][t, r]}, {r, -L, L},
PlotRange -> range, PlotStyle -> {RGBColor[0.3, 0.3, 0.9], Dashed}];
whiteRadial = Table[radial[1 + n*dR], {n, -NR, NR}];
whiteTime = Table[time[n*dT], {n, -NT, NT}];
white = Join[whiteRadial, whiteTime];
redLine =
ParametricPlot[{s, -s}, {s, -W, W}, PlotRange -> range,
PlotStyle -> {RGBColor[1, 0, 0], Dashed, Thick},
AxesLabel -> {"\[Sigma]", "\[Tau]"}];
Show[redLine, black]
Show[redLine, white]
Show[redLine, white, black]



