Дано: Лазерный фотоакустический газоанализатор, имеющий измерительную и опорную газонаполненную ячейки. Лазер своими импульсами продуцирует акустический сигнал в первой и второй ячейках соответственно (измерительная ячейка стоит в луче после опорной). Измеряем норму акустического сигнала в опорной ячейке

и в измерительной

, и, согласно закону Бугера, имеем:

,

,
где

-мощность лазера,

и

- коэффициенты пропорциональности (там "вшиты" усиление по электронике, АЦП и прочие технические прелести),

- коэффициент поглощения,
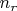
и

- концентрации газа в опорной и измерительной ячейках соответственно,

и

- длины опорной и измерительной ячеек.
Нормируем

на

, получаем:

,
показатель

малый, посему от знаменателя вполне имеем право оставить только показатель, а экспоненту в числителе оставим до кубического члена, соответственно от дроби после сокращений останется (отношение коэффициентов пропорциональности пока вынесем "за скобки"):

теперь, исходя из правомерности замены

на

, можем коэффициент поглощения

записать как:

,
и заменив

в выражении отношения

, а также объединяя все конструктивные константы (концентрация
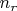
в опорной ячейке, длины, коэффициенты пропорциональности и протчая и протчая) можем записать:

Теперь собственно
Задача.Откалибровать прибор. При калибровке мы можем задуть в измерительную ячейку газ известной нам концентрации (несколько известных концентраций) и измерить

и

при заранее известных

.
Ну а после калибровки, задувая в измерительную ячейку газ с неизвестной концентрацией, получить значения

и

, подставить их в полученную функцию двух переменных и вычислить значение концентрации

.
Проблема: прям-таки математиков (чтоб подсказали как правильно действовать) нету и взять негде, приходится кувыркаться самим.
Вывод: Имея семейство кривых

, надо построить калибровочную поверхность

, аппроксимировать оную поверхность функцией двух переменных и иметь счастье.
Вопросы: 1. В каком специализированном математическом софте это правильнее делать?
2. Очевидно, зависимость (1) резко ограничивает (а может и точно определяет) тип аппроксимирующей функции, не подскажете, каков этот тип?
3. Сетку снятых данных

при шести значениях

и шестнадцати значениях

могу отправить по e-mail, или как-то пристегнуть к сообщению - тока я не знаю как. Экспериментальные данные в картинках пристегну чуть погодя.
P.S.
Решать кубическое уравнение - не вариант, пробовали. Врукопашную в (1) приходится подбирать

, но это, в общем, полбеды, беда в том, что при некоторых измеренных величинах

и

разумного решения

нет (концентрация в комплексных числах - странновато как-то). Плюсом, решение получается крайне неустойчиво относительно этих самых

. Посему, кубическое уравнение решили не решать, а пойти методом калибровочной поверхности.