Вот утверждение и его доказательство:
Let us suppose that probability of success for the treated individual

is

, and

for the untreated. Now, assume that equality
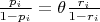
holds for all

and for some
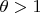
.Therefore:
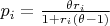
,with
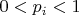
Now, let us define the pooled multiplier
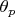
as
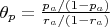
where
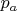
and
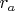
are average values of

and

, respectively.
Proposition 1. Using the notation given above, the following inequality holds

Proof. Suppose
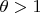
.
Let
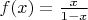
for
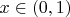
.
So

is a strictly increasing function.
Let
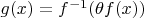
, so
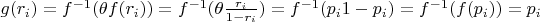
.
The inequality of Proposition 1,

means that
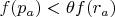
.
As it is shown above
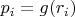
, so we can prove Proposition 1 by proving that function

is strictly concave. But
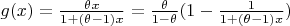
and
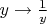
is strictly convex for

.
мне совершенно не понятна последняя часть:
"and
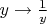
is strictly convex for

"
Можете мне её объяснить? Что это и почему это верно?



