Oleg ZubelevichНасчет выхода на классическое решение. Это же вроде бы известный результат?
За ссылку спасибо, обязательно погляжу. У меня есть Темам, но немного "другой"
"Navier-Stokes equations. Theory and numerical analysis".
Взамен могу указать на явный косяк у Отелбаева. (возможно это будет интересно тем, кто читает его работу).
Лемма 6.10.
Заявляется, что некую величину

можно увеличить. Для этого вводится вспомогательный параметр

. Относительно этого параметра решается некое вспомогательное дифф. уравнение. Результатом и должно стать новое значение

. Отсчет начинается с
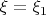
.
Ну так вот. Формула (6.19) дает зависимость

Что такое

и

знать не обязательно. Какие то элементы гильбертова пространства. Какое-то скалярное произведение. Главное, что этот самый

запросто может быть равен 0. Этот случай ПРЯМО оговаривается в конце стр.53. Значит линейная добавка может быть нулевая а поправка неизвестного знака - квадратичная.
Далее, в формуле (6.22) возникает еще одна квадратичная добавка (плюс, возможно, еще что-то более малое)
Ну и, наконец, на стр. 57
"... а из вторых равенств (6.19), (6.22) выводим строгое неравенство

"
Как мы понимаем, вывести не удастся.
Отмечу, что этого следовало ожидать. Дело в том, что в дальнейшем, эта самая

будет выбрана как элемент, на котором достигается максимум некого функционала (квадрат нормы со всякими ограничениями). А значит, градиент этого функционала должен обратиться в 0. Тот самый

как-то сродни этому градиенту, а значит он и должен обратиться в 0.
А вообще, даже если с этим косяком удастся разобраться, не похоже, что такой подход сработает. Очень грубые оценки по норме. Тривиальщина. Я думал, что он внутри где-то решает вспомогательную задачу "с малой нормой". Ну что-нибудь такое.
В предыдущей ссылке (
shwedka указывала ранее) у него было такое утверждение.
Если последовательность правых частей

слабо сходится в

к некой

и для этой

решение гладкое, то для достаточно больших номеров и для

существует гладкое решение.
Вполне содержательное утверждение. Хотя и доказывается сравнительно легко.