Здравствуйте! Недавно столкнулся с опытом Майкельсона и Морли с интерферометром. Преподаватель на лекции частично расписал его для того, чтобы ввести в дело постоянство скорости света (про эфир он ничего не говорил, но эфир меня и не интересует). Вот схема:
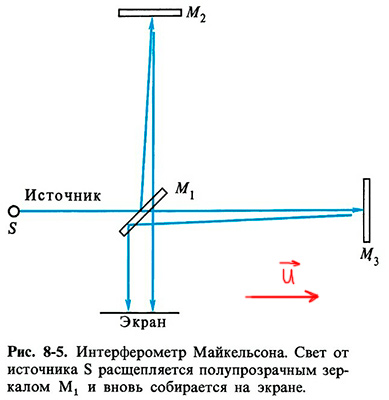
(я думаю, не нужно объяснять, что тут к чему)
Здесь есть вектор скорости

, направленный вправо, - это скорость движения Земли, которая по законам классической механики должна изменить скорость света в системе отсчета неподвижного наблюдателя.
Далее рассматривалось движение света по горизонтальному пути

и по вертикальному пути

. Выражения для времени представляли собой

соответственно. Вот здесь и возникли непонятки. С первым временем всё ясно - это сумма времен при движении света вдоль и противоположно скорости Земли. А вот второе для меня оказалось совершенно неясно. Если

- это длина диагонали, которая получается, если смотреть на путь света от

до

с точки зрения неподвижного наблюдателя, то почему в знаменателе стоит минус, а не плюс? Ведь при движении вверх с точки зрения того же наблюдателя мы вроде должны сложить векторы

и

, и по теореме Пифагора получить для модуля скорости корень из суммы квадратов, а не из разности.
В поисках правды я покопался в интернете и в разных учебниках, но везде формула для

была именно такой (или с вынесенной из-под корня

) и давалась без вывода. Тогда я решил отвязаться от Майкельсона, интерферометра и света вообще, и рассмотреть аналогичную задачу.
Пусть у нас есть тележка, которая едет вправо с постоянной скоростью

. На тележке ящик, на дне которого шарик (на который почти не действует сила тяжести), начинающий движение вертикально вверх с начальной скоростью

, которая и впоследствии остается постоянной. Высота ящика равна

.
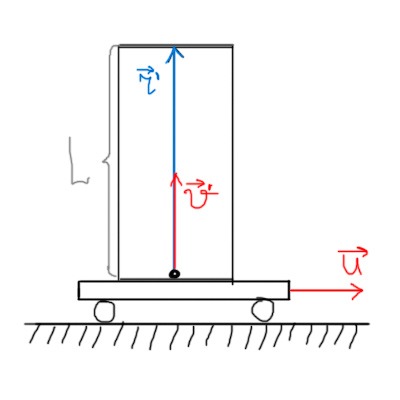
В системе отсчета тележки время движения шарика до "потолка", очевидно,

. Перейдем в неподвижную систему отсчета, используя преобразования Галилея:


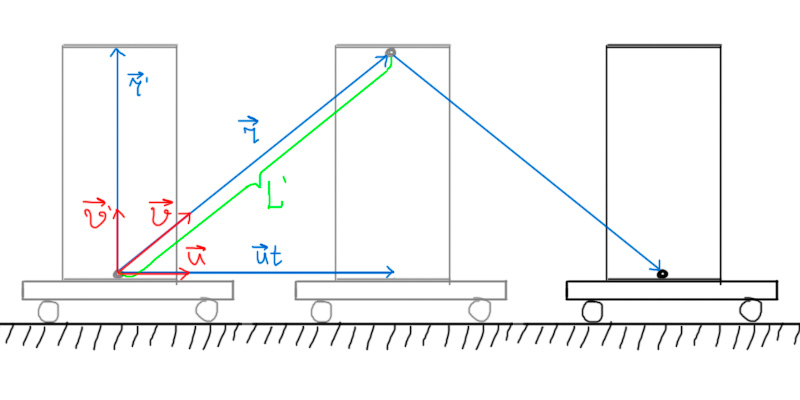
Еще раз найдем время движения шарика до "потолка":


Получили то же самое - значит, преобразования были выполнены верно. Теперь выразим

через диагональ

из рисунка выше:

и подставим в формулу для

:




Если заменить теперь

на

, а

на

и умножить на 2 (я для простоты брал только одну диагональ) то получим то же самое, что было в опыте Майкельсона, но со знаком "+"!
Подскажите, пожалуйста, что я делаю не так? Откуда берется минус?



