На проволочной окружности радиуса

находится надетая на нее маленькая бусина массы

. Коэффициент сухого трения между бусиной и окружностью равен
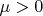
. Бусина насажена на проволоку неплотно. Кольцо неподвижно. Силы тяжести нет.
В момент времени

бусине придали некоторую начальную скорость и предоставили систему самой себе. В момент времени

скорость бусины измерили и нашли, что она равна по модулю

. Оцените сверху время

между "запуском" бусины и моментом измерения скорости.
(Т.е. известны

оценить

)
Релятивистскими эффектами пренебречь
