Кому нужен котангенс?

[migmit]

По названию темы я подумал, что тут продают кота.

[_Ivana]

Развивая подобные идеи, типа "бритва Оккама и ничего лишнего", можно и косинус сразу упразднить за ненадобностью.

[miflin]

_Ivana в сообщении #805063 писал(а):

Развивая подобные идеи, типа "бритва Оккама и ничего лишнего", можно и косинус сразу упразднить за ненадобностью.

В принципе - да.

Но!

При этом основное тригонометрическое тождество будет выглядеть банально:

$\sin^2x+1-\sin^2x=1

А математика - женщина, и должна выглядеть загадочно (как завещал Пифагор):

$\sin^2x+\cos^2x=1

[_Ivana]

Загадочность можно засунуть в смещение аргумента, как оно естественно и гармоническино, а не изощренно с квадратами и корнями. Тогда и основное тождество будет выглядеть не банально, и остальное красиво и естественно.

[miflin]

(Оффтоп)

_Ivana, улыбнитесь, Вас снимают!

[Munin]

_Ivana в сообщении #805063 писал(а):

Развивая подобные идеи, типа "бритва Оккама и ничего лишнего", можно и косинус сразу упразднить за ненадобностью.

Можно. См. "универсальная тригонометрическая подстановка". Или заменой всего на экспоненты.

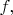
Просто на самом деле, здесь работает не "бритва Оккама", а соображения удобства. Вместо трёх функций $f,$ $\sqrt{1\pm f^2},$ $\sqrt{1\pm f^2}\big/f$ или $f\big/\sqrt{1\pm f^2}$ (иногда только двух из трёх) - часто удобны обозначения типа $\sin,$ $\cos,$ $\tg.$ Или типа $\sh,$ $\ch,$ $\th.$ А вот слишком много таких обозначений - наоборот, заставляют путаться.

(Как вариант, ср. эллиптические функции Якоби: три базовые $\operatorname{sn}u,$ $\operatorname{cn}u=\sqrt{1-\operatorname{sn}^2u},$ $\operatorname{dn}u=\sqrt{1-m\operatorname{sn}^2u},$ и куча производных $\mathrm{ns},\mathrm{nc},\mathrm{nd},$ $\mathrm{sc},\mathrm{sd},$ $\mathrm{dc},\mathrm{ds},$ $\mathrm{cs},\mathrm{cd},$ определяемых как $\langle pq\rangle=\langle pr\rangle/\langle qr\rangle.$ В такой прозрачной нотации и захочешь - не запутаешься.)

Вообще удобство нотации, выработанной и отточенной практикой - великое дело. Удобная нотация не только сильно облегчает расчёты, она ещё и толкает на открытия. Как пример: теория алгебраических уравнений многие века не поднималась выше уравнений 3-4 степени, по той причине, что использовался геометрический язык, и степени неизвестной назывались "квадрат" и "куб" (и "биквадрат"). Введение алгебраической нотации позволило быстро заняться проблемой уравнений $n$-й степени. Заодно, были объединены уравнения с разными знаками при коэффициентах, которые раньше рассматривались как отдельные задачи с разными методами решения.

[arseniiv]

Хочется добавить, что синус и косинус в паре естественны, потому что это проекции результата поворота в плоскости на соответствующим образом выбранные оси (пересечение в центре, длина от центра до оригинала единичная, оригинал лежит на оси, соответствующей косинусу). Правда, синус может получиться не того знака.

-- Пн дек 23, 2013 16:49:11 --

По идее, им должен сопуствовать не тангенс, а арктангенс-2, который по координатам точки выдаёт соответствующий угол.