Лошадь и Кристиан Доплер против СТО.

[jurij]

Лошадь и Кристиан Доплер против СТО.

Великий Ньютон как-то заявил, что «гипотез не измышляем». То есть, по его мнению, физика, кроме как в арифметических аксиомах, в каких либо гипотезах (физических постулатах) не нуждается. Сэр Исаак считал, что математика позволяет вычислить в этом мире ВСЕ с чем, судя по всему согласны современные физики теоретики. По этой причине они глубоко уверены в том, что настоящему физику ничего кроме математики знать не нужно. То есть, по сути, они считают, что физика это не более чем один из разделов прикладной математики. Однако математика это всего лишь инструмент. И если им попытаться заметить физику, то можно попасть впросак, который на полном серьезе воспринимается в одной уважаемой физической теории. Однако давайте по порядку.

Привяжем к столбу лошадь и с помощью динамометра измерим силу, с которой она может тянуть столб. Особо не напрягаясь, животное сможет развить усилие порядка $F =1000$ ньютон. Все, достаточно физики, дальше обратимся к математике.
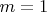
Пусть к лошади привязана гирька массой $m = 1$ грамм. Рассчитаем ускорение, какое она (лошадь) может придать гирьке. Из второго закона Ньютона получим: $F/m = 1000000 m/s^2$. При таком ускорении через 100 секунд лошадь ускорит гирьку до субсветовой скорости.

Внимательный читатель скажет: вот придурок, он же массу лошади в расчете не учел. Виноват, сейчас исправим. Пусть животное имеет массу 200 килограмм. В этом случае массой гирьки можно пренебречь, а лошадь будет двигаться с ускорением $5 m/s^2$. Тоже неплохо, этого ускорения достаточно, чтобы через минуту скорость лошади приблизилась к скорости звука.


Однако опыт показывает, что лошади (даже самые породистые и резвые) с трансзвуковыми скоростями не бегают. Проверяем исходные данные расчета: силу, массу лошади, правильность хода секундомера. Все правильно, а лошадь все равно так быстро не бежит.


В чем тогда ошибка? А в том, что по жизни лошадь бегает от силы со скоростью 15…20 м/с потому, что она лошадь, а не реактивный самолет. Спрашивается, а как учесть это «лошадиное» обстоятельство в расчетах.

А, например, вот так. Обозначим предельную скорость бега лошади как «c». Тогда, как только груз, который ускоряет лошадь, достигнет этой скорости, никакого ускоряющего усилия на него лошадь оказывать не сможет. То есть, сила, с которой лошадь толкает себя, станет равной нулю. Ограниченные возможности лошади можно отобразить так:

$F = F_0 (c - v),$

где v и F – ткущее значение скорости груза и усилия, действующего на него со стороны лошади;
$F_0$ – усилие, которое лошадь создает на неподвижный груз.

С учетом этого второй закон Ньютона следует записать так:

$dv/dt = F_0(c - v)/m. (1) $

Из этого соотношения следует весьма известный вывод: в классической форме закон Ньютона можно использовать лишь при малых скоростях $v << c$. При приближении скорости лошади к «с» возникает «лошадиный» барьер.


Существование «лошадиного» барьера можно объяснить и иначе. Будем считать, что лошадь может бежать сколь угодно быстро. А вот масса груза, который она тянет, зависит от скорости вот так:

$m = m_0/(c - v).$

Если с учетом этого обстоятельства записать второй закон Ньютона, то мы вновь получим соотношение (1). Но эта гипотеза не внушает доверия потому, что никто еще не видел неутомимых лошадей и бесконечно больших жокеев.


Заменим термины: вместо лошади ускоряющая электромагнитная волна в ускорителе элементарных частиц, а вместо гири – элементарная частица. Спрашивается, до какой скорости можно ускорить элементарную частицу в этом ускорителе. По аналогии с лошадью ответ очевиден: до скорости распространения электромагнитной волны в ускоряющем тракте ускорителя и не более. И никаких манипуляций с массой ускоряемой частицы не требуется.


Уважаемая публика может заявить, что аналогия с лошадьми и гирями в таком серьезном вопросе неуместна. Хорошо. Давайте рассуждать более строго. Энергия электромагнитной волны связана с ее частотой так: $W_0 = hn_0$, где h – постоянная Планка, $n_0$ – частота волны в системе отсчета неподвижного наблюдателя. Отсюда, энергия ускоряющей электромагнитной волны в системе отсчета ускоряемой частицы, согласно эффекту Доплера, будет равна:

$W = W_0(c - v).$

Отсюда возникает «лошадиное» ограничение: при $v = с$, энергия ускоряющей волны, в системе отсчета ускоряемой частицы, становится нулевой. То есть по достижению частицей этой скорости никакой энергии волна ей передать не может, а потому рост скорости частицы прекратится.

Можно возразить, что приведенное соотношение записано для классического, а не релятивистского эффекта Доплера. Однако нетрудно убедится, что и в рамках релятивистского эффекта Доплера при скорости движения частицы $v = c$, параметры ускоряющей электромагнитной волны также обнуляются.


Можно заявить, что эффект Доплера показывает суть «светового» барьера с другой стороны и лишний раз подчеркивает, так сказать, глыбину и ширину выводов СТО. Можно и так. Но есть одна закавыка: этот эффект заодно не позволяет передать средствами электромагнитного взаимодействия заряженной частице НЕОГРАНИЧЕННОЕ количество энергии, которое (согласно СТО) является необходимым условием для возникновения «светового» барьера.
Таким образом, есть дилемма. Можно, в рамках ньютоновского формализма, считать, что сила (неважно, лошадиная или электромагнитная) – это независимая величина. Тогда для объяснения наблюдаемого характера движения лошадей на ипподроме и заряженных частиц в ускорителях, следует считать их массу, зависящей от скорости. Соотношениям Доплера в такой концепции не то, чтобы нет места. Просто их следует считать, так сказать, региональными: они описывают свистки паровозов, милиционеров и т.п. чепуху.
А можно считать, что соотношения Доплера имеют универсальный характер. Тогда сомнениям подвергается концепция релятивистской механики, ну а за ней и СТО в целом.
Что выбрать я не знаю. Поэтому прошу наставить меня на путь истинный (по возможности доказательно) уважаемых участников форума.

И еще. Внимательный читатель может возразить. Если СТО такая «нехорошая» теория, то куда девать ее и ОТО эффекты, которые были подтверждены в опытах? Если, уважаемый читатель, Вас это действительно интересует, то Вам сюда: http://www.sciteclibrary.ru/rus/catalog ... 13160.html.
Или сюда:
http://forum.lebedev.ru/viewtopic.php?p=66243#66243.

Здесь будет показано, что существует иной, чем СТО способ описания упомянутых выше эффектов. Причем более общий, поскольку позволяет с единых позиций описать не только эффекты СТО и ОТО, но включит в это же описание магнетизм.

[warlock66613]

jurij в сообщении #804565 писал(а):

$F = F_0 (c - v),$

Размерность не сходится.

[Munin]

Мда, более тупого непонимания СТО я, пожалуй, никогда не видел.

[DLL]

Про лошадь, это пять

[jurij]

warlock66613 в сообщении #804574 писал(а):

Размерность не сходится.

Виноват, $(c - v)$ следует читать как $(1 - v/c)$

[Toucan]

Тема перемещена из форума «Дискуссионные темы (Ф)» в форум «Пургаторий (Ф)»
Причина переноса: более соответствующий раздел.

[Someone]

jurij в сообщении #804565 писал(а):

А, например, вот так. Обозначим предельную скорость бега лошади как «c». Тогда, как только груз, который ускоряет лошадь, достигнет этой скорости, никакого ускоряющего усилия на него лошадь оказывать не сможет. То есть, сила, с которой лошадь толкает себя, станет равной нулю. Ограниченные возможности лошади можно отобразить так:

$F = F_0 (c - v),$

Ну, это, конечно, ерунда, уравнение "срисовано с потолка". Даже если учесть поправку

jurij в сообщении #804584 писал(а):

Виноват, $(c - v)$ следует читать как $(1 - v/c)$

В действительности гораздо интереснее. Кстати, Вы не учли, что в случае лошади на неё действуют всякие силы трения, возрастающие с увеличением скорости, и то, что бедная лошадь не в состоянии двигать ногами со слишком большой скоростью, вследствие чего и сила тяги уменьшается. Но это к теме не относится.

jurij в сообщении #804565 писал(а):

Энергия электромагнитной волны связана с ее частотой так: $W_0 = hn_0$, где h – постоянная Планка, $n_0$ – частота волны в системе отсчета неподвижного наблюдателя. Отсюда, энергия ускоряющей электромагнитной волны в системе отсчета ускоряемой частицы, согласно эффекту Доплера, будет равна:

$W = W_0(c - v).$

Вероятно, имеется в виду та же поправка. Но всё равно это ерунда.

jurij в сообщении #804565 писал(а):

Можно возразить, что приведенное соотношение записано для классического, а не релятивистского эффекта Доплера. Однако нетрудно убедится, что и в рамках релятивистского эффекта Доплера при скорости движения частицы $v = c$, параметры ускоряющей электромагнитной волны также обнуляются.

jurij в сообщении #804565 писал(а):

Спрашивается, до какой скорости можно ускорить элементарную частицу в этом ускорителе. По аналогии с лошадью ответ очевиден: до скорости распространения электромагнитной волны в ускоряющем тракте ускорителя и не более.

Вообще-то, хорошо известно, что скорость света в СТО является недостижимым для массивных частиц пределом скорости, при этом энергия ускоряемой частицы по мере приближения её скорости к скорости света неограниченно возрастает. Поэтому "доказывая", что скорость частицы в ускорителе ограничена скоростью света, Вы ломитесь в открытую дверь.

jurij в сообщении #804565 писал(а):

Можно заявить, что эффект Доплера показывает суть «светового» барьера с другой стороны и лишний раз подчеркивает, так сказать, глыбину и ширину выводов СТО. Можно и так. Но есть одна закавыка: этот эффект заодно не позволяет передать средствами электромагнитного взаимодействия заряженной частице НЕОГРАНИЧЕННОЕ количество энергии, которое (согласно СТО) является необходимым условием для возникновения «светового» барьера.

Этого Вы не доказали. Более того, такой вывод противоречит тем выражениям, которые Вы написали. Если мощность ускоряющего "источника" равна $W_0$, а мощность, "воспринимаемая" ускоряемой частицей, равна, согласно Вашему утверждению, $W=W_0\left(1-\frac vc\right)$, то предположение, что скорость частицы не стремится к скорости света, а ограничена некоторой величиной $v_{\max}<c$, немедленно приводит к противоречию с ограниченностью энергии частицы: так как $v<v_{\max}$, то мощность, "воспринимаемая" частицей, будет $W>W_0\left(1-\frac{v_{\max}}c\right)$, поэтому энергия частицы, полученная за время $t$, будет больше $W_0t\left(1-\frac{v_{\max}}c\right)$, а эта величина, очевидно, неограниченно возрастает со временем.

Можно рассмотреть две модельные задачи. В обеих задачах считаем, что в начальный момент времени $t=0$ скорость $v=0$ и, соответственно, кинетическая энергия $\mathscr E_{\text{кин}}=0$.

Задача № 1. В космическом пространстве на неподвижной платформе установлен мощный лазер, луч которого ускоряет звездолёт, отражаясь от зеркала звездолёта.

Расчёт движения звездолёта имеется в сообщении http://dxdy.ru/post734838.html#p734838, и я его здесь повторять не буду. Но там отсутствуют оценки кинетической энергии звездолёта в зависимости от времени. Формально достаточно подставить выражение (11) в формулу кинетической энергии (5), но получившееся таким образом выражение слишком сложно для непосредственного восприятия. Поэтому следует выписать асимптотические выражения для скорости и кинетической энергии звездолёта при $t\to 0$ и при $t\to\infty$.

На начальном этапе ускорения, когда время $t$ мало, а скорость звездолёта очень мала по сравнению со скоростью света, получаем для скорости звездолёта выражение

$$v\sim\frac{2Wt}{mc}\text{ при }t\to 0,$$

а для его кинетической энергии — выражение

$$\mathscr E_{\text{кин}}\sim\frac{2W^2t^2}{mc^2}\sim\frac{mv^2}2\text{ при }t\to 0.$$

На позднем этапе ускорения, когда время $t$ велико, скорость звездолёта близка к скорости света, а его кинетическая энергия много больше $mc^2$, получаем для скорости звездолёта выражение

$$c-v\sim c\sqrt[3]{\frac{m^2c^4}{18W^2t^2}}\text{ при }t\to+\infty,$$

а для его кинетической энергии — выражение

$$\mathscr E_{\text{кин}}\sim\frac{mc^2}{\sqrt{2\left(1-\frac vc\right)}}-mc^2\sim mc^2\left(\sqrt[3]{\frac{3Wt}{2mc^2}}-1\right)\sim mc^2\sqrt[3]{\frac{3Wt}{2mc^2}}\text{ при }t\to+\infty.$$

Вывод этих соотношений из формул (11) и (5) я не привожу. Студент первого курса, освоивший математический анализ в объёме первого семестра, должен с этим выводом справиться.

Задача № 2. Ускорение заряженной частицы постоянным электрическим полем. Магнитное поле отсутствует.

Я рассмотрю одномерный вариант задачи, когда электрическое поле напряжённости $E$ и скорость частицы $v$ направлены вдоль оси координат $Ox$. Заряд частицы равен $q$. Формулы можно найти в книге [1], § 17. В книге формулы записаны в векторной форме, я же их для рассматриваемого одномерного случая перепишу в скалярной форме:

$$\frac{d\mathscr E_{\text{кин}}}{dt}=qEv,$$

$$\frac{dv}{dt}=\frac{qE}m\sqrt{\left(1-\frac{v^2}{c^2}\right)^3}.$$

Первая формула в книге [1] имеет номер (17.7), а вторая выписана в задаче в конце параграфа для общего случая (в ней нужно положить $\mathbf H=\mathbf 0$ и заменить векторы $\mathbf E$ и $\mathbf v$ скалярными величинами $E$ и $v$).

Из первой формулы сразу следует, что кинетическая энергия частицы

$$\mathscr E_{\text{кин}}=qEvt$$

неограниченно растёт со временем. Проинтегрировав второе уравнение, найдём $\frac v{\sqrt{1-\frac{v^2}{c^2}}}=\frac{qEt}m$, откуда

$$v=\frac{qEct}{\sqrt{(qEt)^2+(mc)^2}}=\frac c{\sqrt{1+\left(\frac{mc}{qEt}\right)^2}};$$

Из последнего выражения также следует, что скорость частицы стремится к скорости света при $t\to\infty$.

Таким образом, несмотря на "лошадиный барьер", в обеих задачах скорость стремится к скорости света, а кинетическая энергия неограниченно возрастает.

Литература.

[1] Л. Д. Ландау, Е. М. Лифшиц. Теоретическая физика. Том II. Теория поля. "Наука", Москва, 1973.