Бифуркационный анализ динамической системы

[aquatko]

Всем привет!
Есть задание, никак не могу понять как его делать, хоть и информации море, особенно англоязычных материалов.
Задание состоит в том, чтобы провести бифуркационный анализ этого дифф. уравнения: $\dot{x}=x^2-x\mu^2$
Точки равновесия, если не ошибся $x=0$ и $x=\mu^2$.
Дальше по идее нужно понять какая из этих точек локально стабильна, а какая нет при разных $\mu$. Но как это делать?
И правильно ли я понял, что это тип "седло-узел"?
Заранее спасибо за любую помощь.

[Otta]

Никаких седел, узлов и т.п. в одномерной ситуации быть не могёт, не путайте.
Устойчивость можно смотреть а хоть по теоремам Ляпунова, чего проще.
Можете вообще его решить, благо оно решается, и смотреть тогда, что и как.

[aquatko]

Спасибо. Если честно, я не понял, а почему не может быть? Я имел в виду седоузловую бифуркацию - http://en.wikipedia.org/wiki/Saddle-node_bifurcation
Тут же одномерная ситуация тоже.

[Otta]

aquatko в сообщении #802445 писал(а):

Я имел в виду седоузловую бифуркацию

Звиняйте, невнимательно прочитала. Седло-узловая бифуркация, конечно, может быть, но почему Вы думаете, что она тут будет? Наличия двух особых точек кое-когда недостаточно.

[aquatko]

В общем, я нашел учебник Strogatz S.H. - Nonlinear Dynamics and chaos with app, здесь написано очень понятным языком и я, кажется, понял как делать это.
Если не сложно, укажите на ошибки.
Ход решения:
$\dot{x}=x^2-x\mu^2$
Приравниваю исходную ф-ю к 0, получаю
$x=x(x-\mu^2)$
Отсюда два корня
$x=0$ и $x=\mu^2$
Построил график(извиняюсь, если непонятно,спросите):
http://cs14113.vk.me/c412216/v412216547/7a2e/PwCkFw8f6bo.jpg (вроде можно же ссылку на график, да?:))
В первом(верхний график) случае $\mu\not=0$, стрелочками обозначил потоки, которые рисуются направо, если $f(x)>0$, и налево, если $f(x)<0$.
Где потоки "встретились", там точка стабильна.
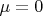
И вот вопрос еще по поводу нижнего графика, где $\mu=0$, где потоки идут в одну сторону, в учебнике написано, что такая точка называется полустабильной, и ее можно считать стабильной(но осторожно ). Правильно ли это?
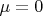
Дальше, как я понял, точка бифуркации это $\mu=0$, так как это единственное место, где пересекаются $x=0$ и $x=\mu^2$.
Ну и в итоге, я решил что это транскритическая бифуркация, так как здесь есть фиксированная точка для всех значений параметра, которая никогда не уничтожается, но может менять стабильность.

[Otta]

aquatko в сообщении #802457 писал(а):

Ну и в итоге, я решил что это транскритическая бифуркация

А почему транскритическая? Где характерная смена устойчивости особых точек при переходе через $\mu=0$? Транскритическая была бы, если бы убрать квадрат у $\mu$ в векторном поле.

aquatko в сообщении #802457 писал(а):

стабильна.

Устойчива, что уж Вы по-английски.

[Oleg Zubelevich]

рисуйте фазовый портрет в расширеном фазовом пространстве $(t,x)$ точнее несколько картинок при разных $\mu$

[aquatko]

Otta в сообщении #802460 писал(а):

А почему транскритическая? Где характерная смена устойчивости особых точек при переходе через $\mu=0$? Транскритическая была бы, если бы убрать квадрат у $\mu$ в векторном поле.

Тогда, если честно, не знаю какая, и самое главное - почему. Было бы хорошо, если бы Вы подсказали.

Oleg Zubelevich в сообщении #802480 писал(а):

рисуйте фазовый портрет в расширеном фазовом пространстве $(t,x)$ точнее несколько картинок при разных $\mu$

У меня получились просто прямые линии $x=...$
Мне кажется я что-то не так сделал.

[Otta]

aquatko
Они не должны все как-то называться. Рисуйте бифуркационную диаграмму, как с Вас просят, и достаточно.

aquatko в сообщении #802457 писал(а):

И вот вопрос еще по поводу нижнего графика, где $\mu=0$, где потоки идут в одну сторону, в учебнике написано, что такая точка называется полустабильной, и ее можно считать стабильной(но осторожно ). Правильно ли это?

Неправильно. Устойчивой ее считать нельзя.
А по поводу названия: допустимо называть полуустойчивой.

[aquatko]

Otta в сообщении #802721 писал(а):

aquatko
Они не должны все как-то называться. Рисуйте бифуркационную диаграмму, как с Вас просят, и достаточно.

Вооо, спасибо большое. Диаграмму попытаюсь нарисовать.

Вопрос еще последний, по поводу точки бифуркации.

aquatko в сообщении #802457 писал(а):

Дальше, как я понял, точка бифуркации это $\mu=0$, так как это единственное место, где пересекаются $x=0$ и $x=\mu^2$.

Я прав?
Заранее спасибо!

[Otta]

А при чем тут пересечение чего-то там? Происходит качественная перестройка фазового портрета, две особые точки слипаются в одну, у той единственной меняется характер устойчивости.
Это надо в динамике представлять себе: вот какой-то большой положительный $\mu$, он непрерывно меняется, двигаясь к нулю, при этом особые точки имеют совершенно определенный тип устойчивости каждая, одна (ноль) стоит, другая движется вправо к нулю, потом - хлоп - в нуле они слиплись и стала одна точка, и тип устойчивости у нее стал не такой, как всегда, потом $\mu$ пошло в отрицательные числа и вторая особая точка тут же отщепилась и пошла вправо, откуда пришла, и тип устойчивости у нее какой был до этого, такой и остался.

Ну и интегральные кривые порисуйте сами для себя, для наглядности, тут это возможно, хоть увидите, что и как. Потому что качественный анализ - это хорошо, особенно это хорошо в "нерешаемых" уравнениях, но не мешало бы знать, как это все выглядит "в природе".

Прямых там никаких нет, конечно.