Запаздывающие потенциалы Лиенара-Вихерта

[ser]

У меня возникает множество вопросов на которые в голову приходят только плохие мысли по выводу формулы для потенциалов Лиенара-Вихерта, который сделал Ландау в Теории поля. Прошу снять мои вопросы в этом выводе. При этом, т.к. у Ландау очень плохо с наглядным объяснением физических явлений, то рисунок я сделаю сам. Так вот Ландау сначала почти нормально ставит задачу

«Согласно формулам запаздывающих потенциалов поле в точке наблюдения $P(x, y, z)$ в момент времени $t$ определяется состоянием движения заряда в предшествующий момент времени $t’$, для которого время распространения светового сигнала из точки нахождения заряда $r_0(t')$ в точку наблюдения $P $ как раз совпадает с разностью ${t}{-t’}$. Пусть $R(t)=r-r_0(t)$ радиус-вектор от заряда $e$ в точку $P$; вместе с $r_0(t)$ он является заданной функцией времени. Тогда момент $t’$ определяется уравнением

$t’+R(t’)/c=t$ (63,1) »

Потом он нам долго рассказывает про мировые линии и четырехвекторы, которыми он по поводу и без повода обильно поливает все свои математические изыски. Но в конце то концов он спускается на грешную землю и заявляет.

«Переходя теперь снова к трехмерным обозначениям, получим для потенциалов поля, создаваемого произвольно движущимся точечным зарядом, следующие выражения:

$\varphi=e/(R-\frac{\vec{V}\vec{R}}{c})$ (63,5)

где $R$ – радиус-вектор, проведенный из точки нахождения заряда в точку наблюдения $P$, и все величины в правых частях равенств должны быть взяты в момент времени $t’$, определяющийся из (63,1).»

В общем-то, формула получилась элементарная и ее можно было получить и без заумных преобразований Ландау с четырехвекторами. Я надеюсь, что из приведенного ниже рисунка всем и так понятно какой должна быть формула для запаздывающего потенциала. На этом рисунке обозначения почти точно совпадают с принятыми у Ландау и я только добавил обозначение угла a между радиус-вектором и вектором скорости заряда и добавил точки 2’’ и 2’’’, а вместо $R(t’)$ в формуле (63,1) написал $R’$. Замечу только, что в настоящий момент времени заряд находится в точке 2 и нам надо найти потенциал в точке $P$, когда заряд находился в точке 2’. При этом заряд движется со скоростью $V $ вдоль оси $X$ и его текущая координата по оси $X $ будет $Vt$, а координаты $Y$ и $Z$ остаются равными нулю.




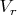
Давайте напишем формулу (1) подобную формуле (63,5) в более понятном для нас виде, что можно сделать просто глядя на рисунок. Здесь у нас будет $dt=t-t’=R’/c$ и $V_r=-V\cos a$ , т.е. $V_r$ это будет скорость изменения радиус-вектора (при допущении, что угол a не изменяется) и в нашем случае она будет отрицательна, т.к. радиус-вектор уменьшается. Но в такой записи у нас получается, что для того, чтобы вычислить $R’$ мы должны знать значение $R’$ (чтобы найти $dt$). Таким образом, мы можем вычислить $dt$ только в первом приближении, как $R/c$ и можем получить аналитическое решение (1) для запаздывания потенциала по координатам только приближенное, даже при условии, что в рассмотренном примере у нас заряд двигался прямолинейно и равномерно и угол a не изменялся, а в общем случае решение будет еще более приближенное. Хотя частное решение мы всегда можем получить, найдя корни квадратного уравнения.

$\varphi=e/(R+V_r dt){\approx}e/R’$ (1)

Поэтому я не понимаю, как удалось Ландау так точно вычислить этот запаздывающий потенциал в общем виде. К сожалению, он при этом даже не объяснил, что это у него за скорость скрывается под буквой $V $ и как она умножается на радиус-вектор $R$, но можно догадаться, что это вектор скорости частицы, а логика подсказывает, что в его формуле (63,5) ) $VR$ это у него скалярное произведение векторов, т.е. можно записать $VR\cos a$ и тогда у него в знаменателе будет $V\cos aR/c$, т.е. тоже самое, что и в формуле (1). Но эта величина у него будет положительной (см. формулу (63,1)) и в результате мы по его формуле (63,5) вычислим потенциал в точке 2’’, т.е. не в прошлый момент времени, а в будущий. Правда, далее, когда Ландау находит напряженности электрического и магнитного полей, он вычисляет $dR(t’)/dt=-V(t’)$ и пишет, что «знак минус здесь связан с тем, что $R$ есть радиус-вектор от заряда e в точку $P$, а не наоборот», т.е. вроде бы все логично и радиус-вектор уменьшается, т.е. в таком случае его формула (63,5) будет идентична нашей формуле (1), но это противоречит его скалярному произведению векторов $VR$ в его формуле (63,5).

Более того, как следует из текста его учебника, который я цитировал выше формула (63,5) у него, оказывается, является не окончательной, т.к. он пишет, что «все величины в правых частях равенств должны быть взяты в момент времени $t’$». Таким образом, окончательно его формула будет выглядеть вот так

$\varphi=e/(R’-(+\vec{V})\vec{R’}/c)=e/R$ (2)

$\varphi=e/(R’-(-\vec{V})\vec{R’}/c)=e/R’’’$ (2’)

И если в этих формулах (2) и (2’) мы берем скорость изменения радиус-вектора в одном случае с плюсом, а в другом с минусом, то мы получаем потенциал или в текущий момент времени (точка 2) или в дважды предыдущий (точка 2’’’), но никак не в предыдущий момент времени (точка 2’). Причем, если следовать буквально его формуле (63,5), то $V$ надо брать с плюсом и в результате мы приходим к формуле (2), т.е. без запаздывания потенциала и, следовательно, это не формула для потенциалов Лиенара-Вихерта.

Обсуждать в этой теме подробности того, зачем ему это надо, я не буду, т.к. я хочу, чтобы, если формула (63.5) не правильная, то мне кто ни будь объяснил, как такую элементарную ошибку никто якобы не заметил за пол века издания его теории поля. Ведь мало того, что никто якобы не заметил этой ошибки, но ведь никто якобы не заметил ее и в преобразованиях Лоренца для потенциала движущегося заряда и в ОТО, где гравитация тоже распространяется мгновенно, т.к. кривизна пространства там изменяется мгновенно, и т.д. А, если формула (63.5) записана правильно, то в чем секрет ее правильного прочтения в окончательном виде (2) или (2’) в соответствии с моим рисунком.

С наилучшими пожеланиями Сергей Юдин.

[photon]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
Тема перемещена в Карантин по следующим причинам:
- неправильное оформление формул

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[photon]

Тема перемещена из форума «Карантин» в форум «Дискуссионные темы (Ф)»
Причина переноса: возвращено после исправлений.

[Munin]

ser в сообщении #798604 писал(а):

Поэтому я не понимаю, как удалось Ландау так точно вычислить этот запаздывающий потенциал в общем виде.

Всё это "вычисление" на самом деле жульничество, потому что точно вычислить эту величину для произвольно движущегося заряда общей формулой нельзя. Можно только вычислить его как решение уравнения, и именно так его Ландау и указал в самом начале параграфа. Для прямолинейного равномерного движения вычислить его можно, но эта задача скучна, Ландау (и Лиенара и Вихерта) интересует решение для движения в общем виде.

ser в сообщении #798604 писал(а):

К сожалению, он при этом даже не объяснил, что это у него за скорость скрывается под буквой $V $ и как она умножается на радиус-вектор $R$, но можно догадаться, что это вектор скорости частицы

Он ввёл 4-скорость частицы $u^k,$ а по введённым ранее обозначениям, $\mathbf{v}$ - это трёхмерная скорость, соответствующая $u^k$ (ф-ла (7.2): $u^i=(\gamma,\mathbf{v}\gamma)$).

ser в сообщении #798604 писал(а):

а логика подсказывает, что в его формуле (63,5) ) $VR$ это у него скалярное произведение векторов

Поразительная догадливость! И много вам пришлось потрудиться, чтобы узнать в лицо стандартное обозначение скалярного произведения?

ser в сообщении #798604 писал(а):

Но эта величина у него будет положительной (см. формулу (63,1))

Нет, из (63.1) не следует, что $\mathbf{vR}$ будет положительной. По (63.1) вообще нельзя судить о направлении вектора $\mathbf{R},$ поскольку там стоит модуль этого вектора (величина, набранная курсивом - модуль вектора, набранного прямым полужирным шрифтом). Знак произведения $\mathbf{vR}$ определяется из определения величины $\mathbf{R},$ которое звучит так:

Цитата:

Пусть $\mathbf{R}(t)=\mathbf{r}-\mathbf{r}_0(t)$ — радиус-вектор от заряда $e$ в точку $P$

и при вашем чертеже будет отрицательным.

ser в сообщении #798604 писал(а):

Таким образом, окончательно его формула будет выглядеть вот так

$\varphi=e/(R’-(+\vec{V})\vec{R’}/c)=e/R$ (2)

$\varphi=e/(R’-(-\vec{V})\vec{R’}/c)=e/R’’’$ (2’)

Это уже ваши ошибки. Разумеется, это вычисление неправильное, $R’-(+\vec{V})\vec{R’}/c\ne R.$

ser в сообщении #798604 писал(а):

Обсуждать в этой теме подробности того, зачем ему это надо, я не буду, т.к. я хочу, чтобы, если формула (63.5) не правильная

Она правильная.

ser в сообщении #798604 писал(а):

А, если формула (63.5) записана правильно, то в чем секрет ее правильного прочтения в окончательном виде (2) или (2’) в соответствии с моим рисунком.

Рисунок надо почистить, а лучше даже нарисовать заново. Тщательно по всем пояснениям Ландау.

Искомая величина в знаменателе, с учётом,
$\dfrac{\mathbf{vR'}}{c}=\dfrac{vR'\cos\alpha(t')}{c}=v(t-t')\cos\alpha(t'),$
будет вот эта вот:

[ser]

Munin в сообщении #799043 писал(а):

Рисунок надо почистить, а лучше даже нарисовать заново. Тщательно по всем пояснениям Ландау.

Искомая величина в знаменателе, с учётом,
$\dfrac{\mathbf{vR'}}{c}=\dfrac{vR'\cos\alpha(t')}{c}=v(t-t')\cos\alpha(t'),$
будет вот эта вот:

Спасибо за уточнение. Действительно в моих формулах (2) и (2’) надо записать в конце не равно, а примерно равно. И таким образом, с учетом Ваших замечаний, у нас остается одна формула (2), и Вы утверждаете, что полученная Ландау формула почти не учитывает запаздывание потенциалов по координатам (потенциалов Лиенара-Вихерта) за исключением малой величины, которую я на рисунке обозначил как $ddR$ . А, если принебречь этой малой погрешностью, то можно утверждать, что формула Ландау для учета потенциалов Лиенара-Вихерта не учитывает потенциалы Лиенара-Вихерта, т.к. потенциал в точке $P$ получается не при воздействии заряда из точки 2’, а при воздействии его из точки 2L, что примерно соответствует положению 2, т.е. текущему положению заряда, т.е. без учета запаздывания.



Конкретно, Вы в своем сообщении показали, что в формуле Ландау в знаменателе радиус $R’$ уменьшается на $ dRL=\dfrac{\mathbf{vR'}}{c}=\dfrac{vR'\cos a’}{c}=v(t-t')\cos a’$ и в этом случае потенциал будет рассчитываться при нахождении заряда в точке 2L. Я же в своем сообщении написал, что при неизменных значениях углов $a$ у нас изменение радиуса $dR=R’-R$ будет равно изменению радиуса у Ландау $dRL$. Но здесь углы $a$ будут отличаться на величину $da$ и поэтому значения $dRL$ и $dR$ будут отличаться на величину $ddR= v(t-t')\sin a’\tg da$. Да, эта погрешность будет не большой, но мне все же следовало в формуле (2) написать

$\varphi=e/(R’-\dfrac{\mathbf{vR'}}{c}){\approx} e/R$ (2)

Таким образом, Ваши пояснения говорят о том, что это не я что-то не так понял у Ландау, а это Ландау вывел не правильную формулу для учета потенциалов Лиенара-Вихерта.

С наилучшими пожеланиями Сергей Юдин.

[Sergeevich]

ser в сообщении #799142 писал(а):

Я же в своем сообщении написал, что при неизменных значениях углов $a$

Не понятно. Как при неподвижной точке Р и движении заряда по прямой (как показано на рисунке) угол $a$ не изменяется? Или Вы имеете ввиду другой угол?

[ser]

Sergeevich в сообщении #799171 писал(а):

Не понятно. Как при неподвижной точке Р и движении заряда по прямой (как показано на рисунке) угол $a$ не изменяется? Или Вы имеете ввиду другой угол?

Естественно, этот угол меняется. Я писал о допущении в двух близко расположенных соседних положениях заряда 2 и 2’, но сейчас я считаю, что об этом допущении не надо было и писать, а надо было сразу определить $ddR$, чтобы не было никаких вопросов.

С наилучшими пожеланиями Сергей Юдин.

[Munin]

ser в сообщении #799142 писал(а):

за исключением малой величины, которую я на рисунке обозначил как $ddR$

Увы, это совсем не малая величина. Отсюда и ваша ошибка.

ser в сообщении #799142 писал(а):

Таким образом, Ваши пояснения говорят о том, что это не я что-то не так понял у Ландау, а это Ландау вывел не правильную формулу для учета потенциалов Лиенара-Вихерта.

Я не знаю, как вам объяснить, что это вы неправильно поняли, а формула, на которую вы смотрите (но не хотите понимать) - правильная. Я вам объяснил настоящий смысл формулы, но вы отмахнулись.

[ser]

Munin в сообщении #799214 писал(а):

Я не знаю, как вам объяснить, что это вы неправильно поняли, а формула, на которую вы смотрите (но не хотите понимать) - правильная. Я вам объяснил настоящий смысл формулы, но вы отмахнулись.

Ну, попробуйте еще раз. Я понимаю так, что формула будет учитывать потенциалы Лиенара-Вихерта, если у нас получится в конечном виде выражение для потенциала движущегося заряда, находящегося в данный момент времени $t$ в точке 2, как потенциал из точки 2’, где заряд был в момент времени $t’$, т.е. будет

$\varphi=e/R’$

И при этом время $dt={t}{-t’}=R’/c$ это время распространения потенциала из точки 2’ в точку $P$ . А у Ландау получилось

$\varphi=e/(R’-dRL)$

Идентичными эти формулы будут только если $V=0$ и, следовательно, $dRL=0$, но это будет формула для поля заряда покоящегося в точке 2’. Что я тут понимаю не так как Вы.

С наилучшими пожеланиями Сергей Юдин.

[Munin]

ser в сообщении #799311 писал(а):

Я понимаю так, что формула будет учитывать потенциалы Лиенара-Вихерта, если у нас получится в конечном виде выражение для потенциала движущегося заряда, находящегося в данный момент времени $t$ в точке 2, как потенциал из точки 2’, где заряд был в момент времени $t’$, т.е. будет

$\varphi=e/R’$

Неправильно. Вернитесь к § 38 "Поле равномерно движущегося заряда", и сравните с настоящими формулами (38.3), (38.4).

И ещё. Лучше не делать, как программисты, и не обозначать величины несколькими буквами ($dRL, dR, ddR$). В математике слитно написанные буквы - это умножение (кроме ещё нескольких особых случаев, например, $d$ может означать дифференциал). Чтобы ввести какие-нибудь дополнительные величины, вы можете их различать штрихами, индексами и т. п.: $R_1,R_2,R_3.$

[Marina_Slavyanka]

ser в сообщении #799311 писал(а):

Munin в сообщении #799214 писал(а):

Я не знаю, как вам объяснить, что это вы неправильно поняли, а формула, на которую вы смотрите (но не хотите понимать) - правильная. Я вам объяснил настоящий смысл формулы, но вы отмахнулись.

Ну, попробуйте еще раз. Я понимаю так, что формула будет учитывать потенциалы Лиенара-Вихерта, если у нас получится в конечном виде выражение для потенциала движущегося заряда, находящегося в данный момент времени $t$ в точке 2, как потенциал из точки 2’, где заряд был в момент времени $t’$, т.е. будет

$\varphi=e/R’$

И при этом время $dt={t}{-t’}=R’/c$ это время распространения потенциала из точки 2’ в точку $P$ . А у Ландау получилось

$\varphi=e/(R’-dRL)$

Идентичными эти формулы будут только если $V=0$ и, следовательно, $dRL=0$, но это будет формула для поля заряда покоящегося в точке 2’. Что я тут понимаю не так как Вы.

С наилучшими пожеланиями Сергей Юдин.

Угу. Ерундой занимаетесь. Сейчас Вам тут накостыляют и забанят в конечном итоге.
ибо это Вам не моя Альтернативка ссылка вырезана //photon

[Sergey K]

(Оффтоп)

Цитата:

ссылка вырезана //photon

АХАХАХАХА!!!! вот где я буду кушать ближайший месяц))) Мергель - это просто чудо и адекватность!

[ser]

Munin в сообщении #799323 писал(а):

Неправильно. Вернитесь к § 38 "Поле равномерно движущегося заряда", и сравните с настоящими формулами (38.3), (38.4).

Я не совсем понял зачем нам здесь нужны преобразования Лоренца для заряда покоящегося в системе отсчета $K’$, которая со скоростью $V$ движется относительно неподвижной системы отсчета $K$. А у нас с Вами в потенциалах Лиенара-Вихерта $V$ это скорость заряда в системе $K’$, а не скорость системы $K’$. Поэтому преобразования Лоренца и запаздывание потенциалов это совершенно разные эффекты. Но, если Вы хотите рассмотреть при запаздывании потенциалов и преобразования Лоренца, то можете это сделать, задавшись скоростью заряда $V$ в движущейся системе отсчета $K’$ и скоростью этой системы $V’$ относительно покоящейся системы $K$. А так Вы используете обозначение $V$ для совершенно разных скоростей.

Munin в сообщении #799323 писал(а):

И ещё. Лучше не делать, как программисты, и не обозначать величины несколькими буквами ($dRL, dR, ddR$). В математике слитно написанные буквы - это умножение (кроме ещё нескольких особых случаев, например, $d$ может означать дифференциал). Чтобы ввести какие-нибудь дополнительные величины, вы можете их различать штрихами, индексами и т. п.: $R_1,R_2,R_3.$

Хорошо, учту на будущее, но Вы действительно угадали, что такие обозначения я использую в своей программе Solsys7mm, где учитываю запаздывание потенциалов по координатам при моделировании движения планет Солнечной системы или двойных пульсаров. Поэтому у меня такие обозначения получаются автоматически (привычка программиста).

С наилучшими пожеланиями Сергей Юдин.

[photon]

Marina_Slavyanka, предупреждение за оффтоп и саморекламу

[Munin]

ser в сообщении #799545 писал(а):

Поэтому преобразования Лоренца и запаздывание потенциалов это совершенно разные эффекты.

Преобразование Лоренца - всего лишь инструмент, чтобы получить потенциал в случае равномерного прямолинейного движения. Чтобы было с чем сравнивать. Вы-то берёте потенциал заряда, находящегося на подходящем расстоянии, но при этом неподвижного - а это ошибка. Заряд, придя в нужную точку, продолжает двигаться. Его поле при этом сжато, и потенциал другой.

Я же вас не тыкаю в формулы преобразований Лоренца выше по параграфу, я указываю конкретно на формулу (38.3). Именно она должна получаться, а не ваша $e/R.$ Разумеется, правильная формула будет равна неправильной $e/R$ только приближённо, но это не проблема правильной формулы - правильная формула остаётся точной сама по себе.

ser в сообщении #799545 писал(а):

А так Вы используете обозначение $V$ для совершенно разных скоростей.

Я его использую только для обозначения скорости заряда. Именно это же значение оно имеет в формуле (38.3). А вывод (38.3) к делу не относится.

ser в сообщении #799545 писал(а):

но Вы действительно угадали, что такие обозначения я использую в своей программе

Да всем плевать.

ser в сообщении #799545 писал(а):

Поэтому у меня такие обозначения получаются автоматически (привычка программиста).

Занимаясь физикой и математикой, будьте любезны пользоваться обозначениями физики и математики. Кто не умеет пользоваться принятым языком - автоматически демонстрирует себя невеждой, и отталкивает окружающих от серьёзного разговора.