The 74th William Lowell Putnam Mathematical Competition
Saturday, 7 December 2013A1Recall that a regular icosahedron is a convex polyhedron having 12 vertices and 20 faces; the faces are congruent equilateral triangles. On each face of a regular icosahedron is written a nonnegative integer such that the sum of all

integers is
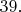
Show that there are two faces that share a vertex and have the same integer written on them.
A2Let

be the set of all positive integers that are
not perfect squares. For

in
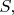
consider choices of integers
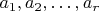
such that
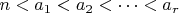
and
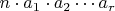
is a perfect square, and let

be the minimum of
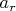
over all such choices. For example,
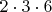
is a perfect square, while

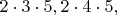
and

are not, and so
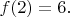
Show that the function

from

to the integers is one-to-one.
A3Suppose that the real numbers
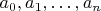
and

with
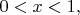
satisfy
![\[\frac{a_0}{1-x}+\frac{a_1}{1-x^2}+\cdots+\frac{a_n}{1-x^{n+1}}=0.\] \[\frac{a_0}{1-x}+\frac{a_1}{1-x^2}+\cdots+\frac{a_n}{1-x^{n+1}}=0.\]](https://dxdy-01.korotkov.co.uk/f/8/7/2/872201219ea79501dff5b794ab3ed26182.png)
Prove that there exists a real number

with
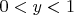
such that
![\[a_0+a_1y+\cdots+a_ny^n=0.\] \[a_0+a_1y+\cdots+a_ny^n=0.\]](https://dxdy-03.korotkov.co.uk/f/e/b/d/ebdc6903f8099e0b034e23310ffb743e82.png) A4
A4A finite collection of digits

and

is written around a circle. An
arc of length
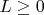
consists of

consecutive digits around the circle. For each arc
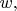
let
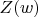
and
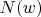
denote the number of

's in

and the number of

's in
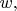
respectively. Assume that
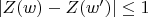
for any two arcs
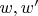
of the same length. Suppose that some arcs

have the property that
![\[Z=\frac1k\sum_{j=1}^kZ(w_j)\text{ and }N=\frac1k\sum_{j=1}^k N(w_j)\] \[Z=\frac1k\sum_{j=1}^kZ(w_j)\text{ and }N=\frac1k\sum_{j=1}^k N(w_j)\]](https://dxdy-04.korotkov.co.uk/f/f/8/c/f8c34e794a71eb71db1321466536651582.png)
are both integers. Prove that there exists an arc

with
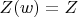
and
 A5
A5For
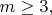
a list of
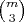
real numbers

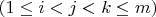
is said to be
area definite for

if the inequality
![\[\sum_{1\le i<j<k\le m}a_{ijk}\text{Area}(\triangle A_iA_jA_k)\ge0\] \[\sum_{1\le i<j<k\le m}a_{ijk}\text{Area}(\triangle A_iA_jA_k)\ge0\]](https://dxdy-03.korotkov.co.uk/f/2/1/6/216b08ae5cff2bae0689790c8240a77f82.png)
holds for every choice of

points

in
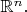
For example, the list of four number
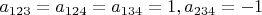
is area definite for
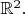
Prove that if a list of
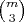
numbers is area definite for
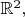
then it is area definite for
 A6
A6Define a function
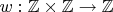
as follows. For
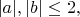
let
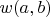
be as in the table shown; otherwise, let
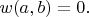
![\[\begin{array}{|lr|rrrrr|}\hline &&&&b&&\\
&w(a,b)&-2&-1&0&1&2\\ \hline
&-2&-1&-2&2&-2&-1\\
&-1&-2&4&-4&4&-2\\
a&0&2&-4&12&-4&2\\
&1&-2&4&-4&4&-2\\
&2&-1&-2&2&-2&-1\\ \hline\end{array}\] \[\begin{array}{|lr|rrrrr|}\hline &&&&b&&\\
&w(a,b)&-2&-1&0&1&2\\ \hline
&-2&-1&-2&2&-2&-1\\
&-1&-2&4&-4&4&-2\\
a&0&2&-4&12&-4&2\\
&1&-2&4&-4&4&-2\\
&2&-1&-2&2&-2&-1\\ \hline\end{array}\]](https://dxdy-03.korotkov.co.uk/f/e/f/a/efaa523f3d6efa1d9f8ae65b52fedc9382.png)
For every finite subset

of
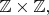
define
![\[A(S)=\sum_{(\mathbf{s},\mathbf{s'})\in S\times S} w(\mathbf{s}-\mathbf{s'}).\] \[A(S)=\sum_{(\mathbf{s},\mathbf{s'})\in S\times S} w(\mathbf{s}-\mathbf{s'}).\]](https://dxdy-03.korotkov.co.uk/f/e/2/1/e21d22f9de37aa667ff8853119e1309f82.png)
Prove that if

is any finite nonempty subset of
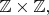
then
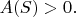
(For example, if
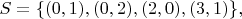
then the terms in
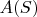
are
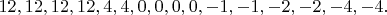
)
B1For positive integers

let the numbers
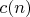
be determined by the rules
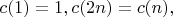
and
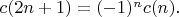
Find the value of
![\[\sum_{n=1}^{2013}c(n)c(n+2).\] \[\sum_{n=1}^{2013}c(n)c(n+2).\]](https://dxdy-04.korotkov.co.uk/f/7/d/c/7dc3788865f10a4171758623b0670a3d82.png) B2
B2Let
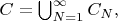
where
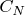
denotes the set of `cosine polynomials' of the form
![\[f(x)=1+\sum_{n=1}^Na_n\cos(2\pi nx)\] \[f(x)=1+\sum_{n=1}^Na_n\cos(2\pi nx)\]](https://dxdy-03.korotkov.co.uk/f/2/b/3/2b3220cc4a0cbfbb119dafb36d75ecd382.png)
for which:
(i)
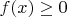
for all real

and
(ii)
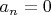
whenever

is a multiple of
Determine the maximum value of

as

ranges through
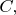
and prove that this maximum is attained.
B3Let

be a nonempty collections of subsets of

such that:
(i) if
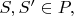
then
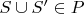
and
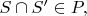
and
(ii) if
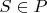
and
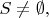
then there is a subset
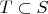
such that
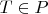
and

contains exactly one fewer element than
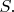
Suppose that
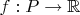
is a function such that
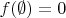
and
![\[f(S\cup S')= f(S)+f(S')-f(S\cap S')\text{ for all }S,S'\in P.\] \[f(S\cup S')= f(S)+f(S')-f(S\cap S')\text{ for all }S,S'\in P.\]](https://dxdy-02.korotkov.co.uk/f/1/f/a/1fa1ebccae0dfa067a421aec6fead51882.png)
Must there exist real numbers

such that
![\[f(S)=\sum_{i\in S}f_i\] \[f(S)=\sum_{i\in S}f_i\]](https://dxdy-02.korotkov.co.uk/f/d/1/f/d1f64bdabeb8d3d583a1ef7b4309e2f082.png)
for every
 B4
B4For any continuous real-valued function

defined on the interval
![$[0,1],$ $[0,1],$](https://dxdy-01.korotkov.co.uk/f/0/a/e/0ae2faac7f0b6f04f2d00a80b1a93c9582.png)
let
![\[\mu(f)=\int_0^1f(x)\,dx,\text{Var}(f)=\int_0^1(f(x)-\mu(f))^2\,dx, M(f)=\max_{0\le x\le 1}|f(x)|.\] \[\mu(f)=\int_0^1f(x)\,dx,\text{Var}(f)=\int_0^1(f(x)-\mu(f))^2\,dx, M(f)=\max_{0\le x\le 1}|f(x)|.\]](https://dxdy-02.korotkov.co.uk/f/5/f/a/5fa57038ca2ad58651a973a22921c4f782.png)
Show that if

and

are continuous real-valued functions defined on the interval
![$[0,1],$ $[0,1],$](https://dxdy-01.korotkov.co.uk/f/0/a/e/0ae2faac7f0b6f04f2d00a80b1a93c9582.png)
then
![\[\text{Var}(fg)\le 2\text{Var}(f)M(g)^2+2\text{Var}(g)M(f)^2.\] \[\text{Var}(fg)\le 2\text{Var}(f)M(g)^2+2\text{Var}(g)M(f)^2.\]](https://dxdy-04.korotkov.co.uk/f/f/9/2/f924d4a2df16cfd906f2629c723dea4482.png) B5
B5Let
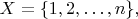
and let
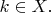
Show that there are exactly
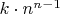
functions
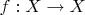
such that for every

there is a
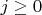
such that
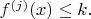
[Here
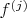
denotes the

th iterate of
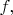
so that
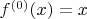
and
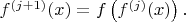
]
B6Let
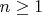
be an odd integer. Alice and Bob play the following game, taking alternating turns, with Alice playing first. The playing area consists of

spaces, arranged in a line. At each turn, a player either

places a stone in an empty space, or

removes a stone from a nonempty space
places a stone in the nearest empty space to the left of

(if such a space exists), and places a stone in the nearest empty space to the right of

(if such a space exists).
Furthermore, a move is permitted only if the resulting position has not occurred previously in the game. A player loses if he or she is unable to move. Assuming that both players play optimally throughout the game, what moves may Alice make on her first turn?
-- Пн дек 09, 2013 20:25:41 --Список городов, где проходило зеркало:
http://putnam.ho.ua/schedule.htmlНекоторые фото:
http://vk.com/album5499034_183760322https://www.facebook.com/dmitry.mitin/m ... 039&type=1



