F. S. Macaulay The algebraic theory of modular systems, Chapter I The resultant, 5. писал(а):
When
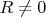
there are
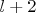
linearly independent members of
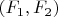
of degree

, and

of degree

. When
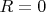
there are only

linearly independent members of degree

and still

of degree

, i.e. in each case 1 less than the number of terms in a polynomial of degree

and

respectively. Hence there will be one and only one identical linear relation between the coefficients of the general member of
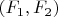
whether of degree

or

.
Как я понял, утверждается, что элементы рассматриваемого идеала степени

при
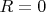
образуют подпространство пространства однородных многочленов коразмерности 1. Но почему так, не понимаю. Помогите разобраться с этим отрывком.
Как правильно оформить ссылку?



