Полиномиальный алгоритм изоморфизма графов

[sup]

В лемме 9 заявлено "$f(M)$ однозначно задает $G_B$", но доказательство отсутствует. А именно. Не показано, что разные $G_B$ непременно дают разные $f(M)$. В сущности, это и есть самый главный вопрос. Как показать, что по набору инвариантов граф восстанавливается однозначно.

[bin]

sup в сообщении #781900 писал(а):

В лемме 9 заявлено "$f(M)$ однозначно задает $G_B$", но доказательство отсутствует. А именно. Не показано, что разные $G_B$ непременно дают разные $f(M)$. В сущности, это и есть самый главный вопрос. Как показать, что по набору инвариантов граф восстанавливается однозначно.

Предположим, что граф $G_{B}$ не изоморфен графу $G_{B}^{\prime}$, но при этом $f(M)=f(M^{\prime})$. Из $f(M)=f(M^{\prime})$ следует, что для каждого графа $\Delta_{i}\in M$ найдется такой граф $\Delta_{j}^{\prime}\in M^{\prime}$, что $\Delta_{i}\cong\Delta_{j}^{\prime}$. Отсюда $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}^{\prime}$. Рассмотрим граф, образованный удалением синего и красного дополнительных корней из $\Delta_{i}$. Этот граф будет равен графу $\Delta_{i}\cap G_{B}$, очевидно, что, удалив из графа $\underset{(i)}{\bigcup}\Delta_{i}$ синие и красные дополнительные корни, получим граф $G_{B}$. Отметим также, что если два $\delta$-графа изоморфны, то графы, полученные удалением их дополнительных корней, также будут изоморфны. Т.о. из $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}$ следует, что $G_{B}\cong G_{B}^{\prime}$, что противоречит нашему предположению, следовательно, оно не верно, и следовательно, если граф $G_{B}$ не изоморфен графу $G_{B}^{\prime}$, то $f(M)\neq f(M^{\prime})$. Т.о. $f(M)$ однозначно задает $G_{B}$.
Спасибо, жду продолжения!

[sup]

bin в сообщении #782474 писал(а):

Т.о. из $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}$ следует, что $G_{B}\cong G_{B}^{\prime}$

Нет, не следует. У нас есть куча "запчастей". Из них можно собрать велосипед, а может и пулемет самокат.
Чтобы понять, что в Вашем доказательстве "не все ладно" можно отметить следующее. Ваша конструкция носит этакий рекурсивный характер. Сначала вершинам приписываются простые коды. Потом с учетом этого кодирования производится новая, более сложная кодировка и так далее. Сколько таких итераций надо сделать? В статье Вы заявляете, что "число итераций в общем случае достаточно ограничить диаметром графа". Но в доказательстве эта величина нигде не фигурирует. Это значит, что Ваши рассуждения от нее не зависят. Иначе где-то бы возникло высказывание типа " ... поскольку количество итераций не меньше диаметра, то ...". С другой стороны, кажется очевидным, что в общем случае количество итераций не может быть слишком малым.
Мне кажется, что без какой-то "нетривиальной" идеи доказать изоморфизм графов по такой схеме не получится. Ну в самом деле. С одной стороны, мы должны строить достаточно сложные инварианты, чтобы учесть возможные "тонкие" различия в графах. С другой стороны, уже после нескольких итераций, конкретное содержание инвариантов становится настолько неосязаемым, что использовать их в доказательстве становится практически невозможным. Позволю себе такое неформальное сравнение. Всем известен рекурсивный стишок "у попа была собака ...". Уже через 2 итерации смысл высказывания совершенно теряется.
Подчеркну, проблема не в том, что инварианты неспособны различать графы, или не дают полиномиальное время работы алгоритма, а в том, чтобы таким образом доказать полиномиальную оценку времени работы.

[bin]

sup в сообщении #782736 писал(а):

bin в сообщении #782474 писал(а):

Т.о. из $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}$ следует, что $G_{B}\cong G_{B}^{\prime}$

Нет, не следует.

Перечитайте, пожалуйста, определения операций объединения и пересечения графов, которые я переписал на стр. 2 из Харари. Если, с помощью какой-либо операции декомпозиции, мы выделим в графе все возможные подграфы, причем во множество этих подграфов входят множества всех вершин и всех ребер исходного графа, то самоочевидно, что обратная операция объединения этих подграфов даст исходный граф. Для того чтобы понять этот факт, следует учесть, что речь идет о помеченном графе, т.е. графе, в котором вершины и ребра пронумерованы. Т.о. пересечение двух подграфов м.б. не пусто, иначе об операции пересечения не было бы никакого смысла говорить, т.к. ее результатом всегда был бы пустой граф.

sup в сообщении #782736 писал(а):

У нас есть куча "запчастей". Из них можно собрать велосипед, а может и пулемет самокат.

Неудачная аналогия. С топологической точки зрения самокат и велосипед - одно и тоже: у них руль, два колеса и "седло", на котором можно стоять или сидеть, а так же рама, все это соединяющая. С геометрической точки зрения самокат из велосипеда не сделать: слишком большой диаметр колес, и слишком маленькое седло - две ноги не поставить. Из практики мы знаем, что из велосипеда можно собрать только велосипед

sup в сообщении #782736 писал(а):

Ваша конструкция носит этакий рекурсивный характер.

Без "этакий". Рекурсия видна в определении 3: строки 6,7.

sup в сообщении #782736 писал(а):

В статье Вы заявляете, что "число итераций в общем случае достаточно ограничить диаметром графа". Но в доказательстве эта величина нигде не фигурирует.

Очевидное ограничение: на каждой итерации вершина получает код инцидентных ребер, а ребро код инцидентных вершин, т.о. через одну итерацию каждая вершина получает код соседних вершин, еще через одну код соседей этих соседей и т.д. Как только максимально удаленные вершины получат коды друг друга итерации можно прекращать: ничего нового о других вершинах никакая вершина не узнает (ср. с алгоритмом изоморфизма деревьев: начинаем с листьев, двигаясь к корню). Диаметр фигурирует в оценке сложности.

sup в сообщении #782736 писал(а):

Мне кажется, что без какой-то "нетривиальной" идеи доказать изоморфизм графов по такой схеме не получится. Ну в самом деле. С одной стороны, мы должны строить достаточно сложные инварианты, чтобы учесть возможные "тонкие" различия в графах. С другой стороны, уже после нескольких итераций, конкретное содержание инвариантов становится настолько неосязаемым, что использовать их в доказательстве становится практически невозможным. Позволю себе такое неформальное сравнение. Всем известен рекурсивный стишок "у попа была собака ...". Уже через 2 итерации смысл высказывания совершенно теряется.

Нет, есть известный факт, описанный в книге Зыкова, на которую я ссылаюсь: полные инварианты кода матрицы смежности (КМ). Для того чтобы получить КМ, нужно, начиная с первого элемента матрицы двигаясь слева направо и сверху вниз, выписывать в строчку нули и единицы. Полученное двоичное число есть КМ. Перебрав все перестановки матрицы смежности, получим минимальный КМ (миникод) и максимальный КМ (максикод). Для изоморфизма графов необходимо и достаточно, чтобы их миникоды и максикоды были соответственно равны. Недостаток этого алгоритма в том, что ему нужен факториал переборов Другой факт (который я использую): изоморфизм деревьев решается через корневые кортежи.

sup в сообщении #782736 писал(а):

Подчеркну, проблема не в том, что инварианты неспособны различать графы, или не дают полиномиальное время работы алгоритма, а в том, чтобы таким образом доказать полиномиальную оценку времени работы.

Для деревьев и планарных графов это доказано (у меня приведены ссылки). Думаю надо следовать той же методике. Конечно проблема очень сложная, иначе ее давно бы решили. (Я, нпр., занимаюсь этой проблемой далеко не первый год.) Дополнительным осложняющим обстоятельством является совершенно естественная предвзятость у каждого, кто читает статью, подобную моей, с попыткой решения этой проблемы. Попробуйте перешагнуть через эту предвзятость

[sup]

bin в сообщении #783051 писал(а):

то самоочевидно, что обратная операция объединения этих подграфов даст исходный граф

Не очевидно. Объединение - суть некий набор подграфов. Чтобы по ним как-то восстановить исходный граф надо их как-то между собой склеить по вершинам и ребрам (поскольку они там встречаются во множественном числе). Если каждый подграф уникален и единственным образом соединяется с другими - то да. Сборка произойдет сама собой. А если там есть одинаковые? Или их можно склеивать разными способами. Не забудем, что это лишь "малые" фрагменты (их то я и назвал "запчастями"). Кого с кем склеивать? Не знаю как Вам, а мне не очевидно. Чтобы это почувствовать в полной мере достаточно вывалить кому-нибудь всю эту кучу подграфов с их зубодробительными кортежами и предложить "очевидным образом" склеить. (Разумеется, нужна не сама склейка, а доказательство ее возможности единственным способом). Вот тут-то и видно, какую тяжелую проблему порождает эта рекурсия. Совершенно не понятно, какие ситуации там могут возникать, а какие нет. Что там будет происходить, что там уникально,а что нет, что там можно склеить, а что нельзя - невозможно предугадать. Навскидку работают только простейшие соображения типа "закон сохранения массы", но хватит ли их - непонятно. В любом случае, для формального доказательства нужна некая процедура склейки или доказательство того, что она не потребуется. Вы ее не предъявляете, ссылаясь на очевидность. Мне кажется, что если таковая есть, то это ничто иное как сериализация и десериализация объекта. В этом случае и огород городить не зачем.
Не думайте, что это голая придирка. Ну давайте попробуем.
Вот взяли какой-то подграф. Попробуем к нему что-то подклеить. По принципу совпадения кодов вершины. Нашли что-то, подклеили. Еще подклеили. И вдруг видим, что вот деталька, ее можно приклеить и так и так, но получатся РАЗНЫЕ графы. Вот и развилка. Что делать? Либо доказывать, что одна из веток заведет в тупик (а значит не стоит нашего внимания), либо доказывать, что такая развилка никогда не появится. Ни один из этих вариантов не выглядит очевидным. И у Вас на этот счет ничего нет. Откуда уверенность, что такого не случится?

bin в сообщении #783051 писал(а):

Очевидное ограничение: на каждой итерации вершина получает код инцидентных ребер, а ребро код инцидентных вершин, т.о. через одну итерацию каждая вершина получает код соседних вершин, еще через одну код соседей этих соседей и т.д. Как только максимально удаленные вершины получат коды друг друга итерации можно прекращать: ничего нового о других вершинах никакая вершина не узнает (ср. с алгоритмом изоморфизма деревьев: начинаем с листьев, двигаясь к корню). Диаметр фигурирует в оценке сложности.

Ну Вы же понимаете, что это называется не доказательство, а правдоподобные рассуждения. Как Вы узнали, когда вершины еще получают новую информацию, а когда уже нет? А почему вершина узнает что-то новое на последнем шаге ...? Ну том, который на 1 меньше диаметра? Может и на нем она ничего нового не узнает? Тогда количество итераций можно еще уменьшить. А потом снова задать этот вопрос. Но тогда получится что, можно дойти вообще до одной или двух итераций, где уже здравый смысл начнет подсказывать, что тут что-то не в порядке. А может и наоборот. Найдется такой странный граф, что и на шаге "диаметр+1" вершины будут узнавать что-то новое. Тогда количество итераций придется увеличивать. Но и это плохо. Тогда поплывет оценка сложности. Вы видите, что вопрос этот совсем не праздный. Откуда Вы знаете, что этот процесс не будет продолжаться сколь угодно долго? Или не "устаканится" через несколько шагов? Сколько же итераций на самом деле нужно? Судя по Вашим словам, Ваш опыт говорит: "Хватит и диаметра. До сих пор хватало ...". Ну что-ж. Не буду спорить. Но это не доказательство того, что хватит всегда. Повторю, проблема не в том, что эта процедура не способна решить задачу. Проблема в формальном доказательстве. В формальном доказательстве Вам потребуется обосновать конкретную величину - количество итераций. Вы ее может положить равной чему угодно. Например диаметру или двум диаметрам. И можете даже не объяснять, почему именно этому, а не чему-то другому. Захотелось и все. Но если в доказательстве эта величина никак не участвует (а в Вашем доказательстве она не участвует), значит она не имеет никакого значения и ее можно положить равной чему угодно, например 1 или 2. Выдержит Ваше доказательство такой выбор?
Насчет предвзятости. У меня нет никакой предвзятости. Я не специалист по графам и у меня нет ревности, что кто-то решил трудную проблему, а я нет. Но сама проблема мне интересна и был бы рад увидеть, что кто-то ее решил. Ваша конструкция достаточно громоздкая, чтобы ссылаться на очевидность. А косвенные соображения (навроде количества итераций) прямо указывают на то, что формальное доказательство отсутствует или, по меньшей мере, не полно.

[bin]

sup в сообщении #783059 писал(а):

Не думайте, что это голая придирка.

Не думаю! Напротив, ради таких "придирок" и затеяно это обсуждение, и выбрана форма препринта, а не статьи в журнале. Но и Вы, в свою очередь, не думайте, что я пытаюсь отмахнуться от какого-либо из Ваших замечаний. Ok?
Про объединения и пересечения. Дан граф $G$, пронумеруем его вершины $1,2,...,n$ и ребра $1,2,...,m$.

Сначала выделим из этого графа два подграфа:
1) вершины $\{1,2,...,k\}$, ребра $\{1,2,...,t\}$,
2) вершины $\{k+1,...,n\}$, ребра $\{s,...,m\}$,
где $t<s<m$.
Пересечение этих подграфов будет пустым графом.
Объединение этих подграфов даст несвязный граф с вершинами $\{1,2,...,k,k+1,...,n\}$ и ребрами $\{1,2,...,t,s,...,m\}$.

Теперь выделим из графа $G$ два подграфа:
1) вершины $\{1,2,...,k\}$, ребра $\{1,2,...,t\}$,
2) вершины $\{k,...,n\}$, ребра $\{t+1,...,m\}$.
Пересечением этих подграфов будет граф, не имеющий ребер и состоящий из одной вершины $k$.
Объединение этих подграфов даст исходный граф $G$. Согласны? И где здесь проблема сборки? Давайте разберемся с этим, а потом я продолжу свой ответ.

[sup]

Что-то я засомневался, в каком контексте задан этот вопрос.
Я правильно понимаю, что данные два подграфа уже получены некой склейкой и мы проводим следующий шаг? Если это так, то да, здесь проблемы нет. Склейка происходит единственным образом.

[bin]

sup в сообщении #783330 писал(а):

Что-то я засомневался, в каком контексте задан этот вопрос.
Я правильно понимаю, что данные два подграфа уже получены некой склейкой и мы проводим следующий шаг? Если это так, то да, здесь проблемы нет. Склейка происходит единственным образом.

Чтобы ответить, придется сделать небольшое методологическое "отступление". Посмотрите, как интересно получается: у нас есть строгое определение объединения графов, и в "дано" ничего не сказано о том, что искомые подграфы уже были как-то получены. Однако для понимания этого кажется недостаточным и при переходе на понятийный уровень появляется избыточное слово "склейка", для которого в нашем обсуждении не прозвучало строгого определения. Из контекста в общем-то понятно, что Вы имеете в виду, поэтому можно ответить "Да" (хотя, например, неясно, чем, в таком случае, склейка будет отличаться от объединения). И это нормальная практика. Обычно обсуждение решений нетривиальных проблем происходит на двух параллельных уровнях: на строгом и на понятийном. Читателю и критику это дает возможность убедиться, что он действительно правильно понял, а автору, помимо прочего, это дает идеи необходимых пояснений в следующую версию обсуждаемого текста - ведь важно не только строго доказать решение, но сделать это понятно для целевой аудитории. Но при этом нужно помнить и об опасностях, которые несет обсуждение на двух уровнях. Одной из них является гипотетическая возможность подмены термина, например, замена "объединение" на "склейка" может сделать возможным опровержение другой части моего доказательства

Итак, я отвечаю утвердительно (с учетом сделанных оговорок). Снимает ли это Ваши возражения по дополнению к Лемме 9, которое я сделал выше?

[sup]

Ну что-же, виноват, похоже, что был не прав. Но возражения не снимаются, а лишь сдвигаются в другое место.
Я ошибочно полагал, что $\bigcup \Delta_i $ означает просто множество неких подграфов. В этом случае запись $\bigcup \Delta_i \cong \bigcup \Delta'_i$ означала бы, что это просто два множества, состоящие из изоморфных графов: каждому $\Delta_i$ соответствует некий $\Delta'_j$ (и это соответствие взаимно-однозначно). Тогда и возникает вопрос, почему из одинакового набора подграфов можно однозначно восстановить (склеить) исходный граф.
Но Ваше определение уже предполагает, что одинаковые вершины и ребра отождествлены, а значит никакой склейки не требуется. Если я правильно понимаю, то это объединение отличается от исходного графа лишь дополнительными корнями и ребрами, им инцидентными.
Но тогда вопрос: а откуда Вы взяли, что $\bigcup \Delta_i \cong \bigcup \Delta'_i$?
Вот Вы пишете

bin в сообщении #782474 писал(а):

Предположим, что граф $G_{B}$ не изоморфен графу $G_{B}^{\prime}$, но при этом $f(M)=f(M^{\prime})$. Из $f(M)=f(M^{\prime})$ следует, что для каждого графа $\Delta_{i}\in M$ найдется такой граф $\Delta_{j}^{\prime}\in M^{\prime}$, что $\Delta_{i}\cong\Delta_{j}^{\prime}$. Отсюда $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}^{\prime}$.

Как Вы это получили?
К слову. Поскольку Вас сейчас интересует лишь сам факт полиномиальности алгоритма, то предлагаю в дальнейшем считать графы $G$ и $G'$ двудольными. Это не умаляет общности, зато позволяет начисто избавиться от зеленых деревьев.

[bin]

sup в сообщении #784105 писал(а):

Но Ваше определение уже предполагает, что одинаковые вершины и ребра отождествлены, а значит никакой склейки не требуется. Если я правильно понимаю, то это объединение отличается от исходного графа лишь дополнительными корнями и ребрами, им инцидентными.

Да.

sup в сообщении #784105 писал(а):

bin в сообщении #782474 писал(а):

Предположим, что граф $G_{B}$ не изоморфен графу $G_{B}^{\prime}$, но при этом $f(M)=f(M^{\prime})$. Из $f(M)=f(M^{\prime})$ следует, что для каждого графа $\Delta_{i}\in M$ найдется такой граф $\Delta_{j}^{\prime}\in M^{\prime}$, что $\Delta_{i}\cong\Delta_{j}^{\prime}$. Отсюда $\underset{(i)}{\bigcup}\Delta_{i}\cong\underset{(i)}{\bigcup}\Delta_{i}^{\prime}$.

Как Вы это получили?

Пусть $G_1=(V_1,E_1), G_2=(V_2,E_2), H=G_1 \bigcup G_2$. По определению: $H=(V_1 \bigcup V_2 , E_1 \bigcup E_2)$. Объединение множеств (нпр., $V_1 \bigcup V_2 $), по определению операции объединения, дает единственный результат (нпр., $\{1,2,3\} \bigcup \{3,4,5\}=\{1,2,3,4,5\}$; аналогичный пример можно привести и для ребер). Т.о. смежность (несмежность) при объединении сохраняется, т.е., если, нпр., в $G_1$ и/или в $G_2$ было (не было) ребро $(1,2)$, то и в графе $H$ будет (не будет) это же самое ребро, соответственно. Изоморфизм - это соответствие, сохраняющее смежность (первая фраза препринта из книги Харари).

[sup]

Виноват, но я не понял. А где в этих рассуждениях $\bigcup \Delta_i$ и $\bigcup \Delta'_i$?
Или Вы на примере двух графов показываете как получается изоморфизм?

[bin]

sup в сообщении #784614 писал(а):

Виноват, но я не понял. А где в этих рассуждениях $\bigcup \Delta_i$ и $\bigcup \Delta'_i$?
Или Вы на примере двух графов показываете как получается изоморфизм?

Далее доказывается индукцией. Но в другом должен с Вами согласиться: нужно подчеркнуть, что вышесделанные мною утверждения справедливы только в контексте леммы 9. Из изоморфизма подграфов $\Delta_i, \Delta'_i$, полученных описанной в препринте декомпозицией, следует $\bigcup \Delta_i$ и $\bigcup \Delta'_i$, а вот для графов "вообще", некоторые из которых могут быть и подграфами, этого не следует. Возьмем, нпр., $C_3$ и $C_4$ ("треугольник" и "квадрат"), в одном случае из них можно построить "домик" (две вершины у подграфов общие), а в другом "домик со съехавшей крышей" (только одна вершина общая). Третий случай - "с домика снесло крышу" (нет общих вершин) Заметим, что общее число вершин графа во всех случаях различно, а в последнем случае граф несвязный, т.о. к лемме 9 этот пример не относится, но о формулировках безусловно надо подумать.

[sup]

bin в сообщении #785102 писал(а):

нужно подчеркнуть, что вышесделанные мною утверждения справедливы только в контексте леммы 9. Из изоморфизма подграфов $\Delta_i, \Delta'_i$, полученных описанной в препринте декомпозицией, следует $\bigcup \Delta_i$ и $\bigcup \Delta'_i$, а вот для графов "вообще", некоторые из которых могут быть и подграфами, этого не следует.

Вот это и есть главный вопрос. Почему в условиях леммы справедливы, если в общем случае нет? Что такое особенное в ситуации леммы 9, что позволяет сделать такой вывод? В Вашем тексте не сказано решительно ничего. Вы приводите простой пример с треугольником и квадратом. Разные варианты склейки (!) этих подграфов приводят к графам с разным количеством вершин. Но если взять шестиугольник и два треугольника и потребовать склейки каждого треугольника с шестиугольником по ребру, то такое простое соображение не срабатывает. Разумеется, и в этом случае легко указать инвариант, который отсечет один из вариантов. Но где гарантия, что это всегда возможно? Можно привести еще более простой пример. Возьмем два графа с одинаковым количеством вершин и ребер и разберем их на отдельные ребра (=подграфы). Ясно, что без привлечения разметки вершин уже никак не обойтись. Но как это сделать? Особенно с учетом непрозрачности используемых инвариантов. Полагаю, что формальное доказательство будет весьма трудным (если вообще возможно). Вот в нем наверняка и появится необходимая глубина рекурсии, о которой я уже говорил.

[bin]

sup в сообщении #786354 писал(а):

Почему в условиях леммы справедливы, если в общем случае нет? Что такое особенное в ситуации леммы 9, что позволяет сделать такой вывод?

Потому, что если мы "разбираем" граф, т.е. выделяем в нем пографы (как в лемме 9), не теряя вершин и ребер, то, как я уже отметил выше, "собрать" его можно единственным образом, а вот если мы берем некоторые графы, то "склеить" из них новый граф можно как угодно. В первом случае пересечение подграфов не пустое, а во втором всегда пустое. В этом особенность.

sup в сообщении #786354 писал(а):

Ясно, что без привлечения разметки вершин уже никак не обойтись. Но как это сделать?

Я и использую разметку. Более того, у меня три разметки - собственно инварианты, номера вершин, номера ребер. Номера вершин и ребер задают однозначный результат "сборки", т.е. однозначный результат для объединения и пересечения подграфов. Возможно, что можно предложить и другой метод. Например, если мы перечислим все возможные остовные деревья, сохраняя первоначальную нумерацию вершин и ребер, то их объединение, видимо, даст исходный граф. Но перечисление всех таких деревьев в общем случае будет очень трудоемким по вычислительной сложности.

sup в сообщении #786354 писал(а):

Особенно с учетом непрозрачности используемых инвариантов.

Тут я не понял: кортежирование вершин дерева, описанное Зыковым и др., дает прозрачные инварианты?

sup в сообщении #786354 писал(а):

Но если взять шестиугольник и два треугольника и потребовать склейки каждого треугольника с шестиугольником по ребру, то такое простое соображение не срабатывает.

И это не понял: что должно происходить с вершинами при "склейке по ребру"? Они все разные у многоугольников или есть и общие? Если все разные, то и ребра все разные и не может быть общего ребра для склейки. А если есть общие, то склейка будет давать единственный результат (см. выше).

[sup]

Прозрачность или непрозрачность объекта понятие, конечно-же, субъективное. Но, в конечном итоге, означает, какие свойства этого объекта мы можем использовать в рассуждениях, и насколько легко. Чем больше этих свойств, чем легче они для восприятия, тем легче нам манипулировать этими объектами и, в конечном итоге, доказывать некие теоремы.
Кортежирование дерева и Ваше кортежирование весьма похожи по форме, но здорово отличаются по их использованию. Поэтому, то, что достаточно для деревьев, не достаточно в Вашем случае, а значит нужны доп. свойства. Давайте посмотрим.
В кортежировании деревьев установлен частичный порядок на вершинах (уровни, и ребра). Кортеж вершины - это упорядоченный набор кортежей вершин лежащих ниже. Для доказательства изоморфизма этого единственного свойства и достаточно. Обращаю Ваше внимание, что предварительно устанавливается некий специальный порядок. Без него кортежирование даже не определяется. У каждой вершины кортеж ровно один. По индукции (начиная с висячих вершин) можно показать, что совпадающие кортежи означают, что Х-деревья (дерево вершин "меньше-или-равных" данной) этих вершин изоморфны.
Ну а теперь посмотрим что у Вас. Никакого порядка на вершинах не установлено. Как следствие, Вы вынуждены перебирать все возможные "корни" ( Ваша декомпозиция у деревьев - это в точности выбор корня). Но теперь у Вас не один кортеж на вершину, а целая пачка. Тут же вопрос - как они связаны между собой? Ясно, что они не могут быть уж совсем какие-попало. Но что их связывает? Ну да, степень вершины должна быть одна и та же, ну может еще что-нибудь такое же. Но на первый взгляд больше ничего и не видно. А связи то нужны. Почему? Да потому, что Вы намерены эти комплекты кортежей использовать в доказательстве. Без связей это все равно, что манипулировать каждым кортежом ПО ОТДЕЛЬНОСТИ. А по отдельности изоморфизм не доказать. Вот это и есть то, что я называл непрозрачностью. Вроде бы и свойства есть, а пользоваться ими не так-то и легко.
Далее. Насчет склейки. То, что из набора подграфов исходный восстанавливается - и спору нет. Нумерация вершин и ребер достаточна для этого. Кортежи для этого не нужны. Но если исходить ТОЛЬКО из изоморфности подграфов с кортежами, то единственность под вопросом. Я не знаю верно это утверждение или нет, но доказательство Вы не предъявили. Ну в самом деле пусть даны два комплекта попарно изоморфных подграфов $\Delta_i \cong \Delta'_i$.
Пусть
$\Delta_1$ - ребро с номером 1 и вершинами 1,2, кортежи $\alpha$, $\beta$.
$\Delta_2$ - ребро с номером 2 и вершинами 1,3, кортежи $\alpha$, $\gamma$,.
$\Delta'_1$ - ребро с номером 10 и вершинами 10,11, кортежи $\alpha$, $\beta$.
$\Delta'_2$ - ребро с номером 11 и вершинами 12,13, кортежи $\alpha$, $\gamma$.
Эти графы, очевидно, попарно изоморфны.
Начинаем "восстанавливать" исходный граф. Взяли пару изоморфных подграфов и склеиваем их по одинаковым вершинам и ребрам. $\Delta_1$ и $\Delta_2$ склеились по общей вершине, а вот $\Delta'_1$ и $\Delta'_2$ - нет. И все. Дорожки разбежались. Что там получится в самом конце, когда мы используем все подграфы - не известно. Вы, конечно, можете возразить, и сказать, что это невозможно и кортежи вершин должны быть разными, а значит изоморфизма помеченных графов то и нет. Ну что-ж, может быть и разные, а может и одинаковые. Я не знаю, а Вы не обосновываете (в общем случае). Этот пример весьма прост, и в нем легко разобраться, а что делать в "общем случае"? Дело то все в том, что я привел лишь иллюстрацию моих сомнений. А вот Вам предстоит предъявить строгое доказательство того, что такое невозможно в самом общем случае.
Далее. Вы утверждаете, что изоморфизм получается по индукции. Но Вы даже не сформулировали индукционное утверждение.
Что мы будем доказывать по индукции? Судя по всему, утверждение выглядит так.
Положим $G_i = \bigcup \limits_{j \leqslant i}\Delta_j$, $G'_i = \bigcup \limits_{j \leqslant i}\Delta'_j$
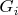
Тогда, для всякого $i$ графы $G_i$ и $G'_i$ изоморфны. База есть. При $i=1$ утверждение верно. А дальше? Уже следующий шаг не слишком очевиден. Пример я уже приводил. Нужны Ваши рассуждения.