Динамика. Задача на Блоки и не ИСО.

[Pripyat]

Добрый день, не уверен в решении, в правильности ходов. Помогите, пожалуйста, разобраться.

Цитата:

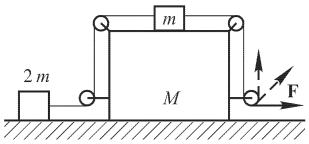
Условие: Найдите ускорения грузов 2m, m и М в системе, показанной на рисунке. Трением пренебречь. Рассмотрите три случая:
а) сила F направлена горизонтально;
б) сила F составляет угол $\alpha$ с горизонтом;
в) сила F направлена вертикально вверх.


Ответ:
а) $a_{2m}=a_m=\frac{F}{3m},~ a_M=0$
б) $a_{2m}=a_m=\frac{F}{3m},~ a_M=-\frac{F}{M}(1-\cos\alpha)$
в) $a_{2m}=a_m=\frac{F}{3m},~ a_M=-\frac{F}{M}$

(Задачник по физике, Белолипецкий, Еркович, №1.180)

Предполагаемое решение:
Потянув за нить мы начинаем двигать грузы m и 2m, жёстко связанных нитью. Расстояние между грузами m и 2m всегда будет одинаково. Таким образом, $a_m=a_{2m} = \frac{F}{2m+m}=\frac{F}{3m}$.

Рассмотрим систему центральный брус + груз m. Будем считать, что сила F под углом $\alpha$, тогда для случая а) $\alpha = 0^\circ$, для случая в) $\alpha = 90^\circ$.
Тогда в горизонтальном направлении на центральный брус действует на правый блок сила $F\cos\alpha$, а на левый блок сила натяжении второй нити $~T$.
Рассмотрим груз 2m и найдём T: $T = 2m\cdot a_{2m} = 2m\cdot \frac{F}{3m} = \frac{2F}{3}$.

Чтобы рассмотреть систему центральный брус + груз m, я ввожу силу инерции $F_i = -m\cdot a_{\text{пер}}$ для груза m.
$a_{\text{пер}}=a_m-a_{\text{отн}}=a_m-a_M$.

Тогда, запишем уравнения динамики для системы Брус+Груз m.
$(M+m)a_M = F\cos\alpha - T - F_i$
$(M+m)a_M = F\cos\alpha - \frac{2F}{3} - m(a_m-a_M)$
$(M+m)a_M = F\cos\alpha - \frac{2F}{3} - m(\frac{F}{3m}-a_M)$
$Ma_M+ma_M = F\cos\alpha - \frac{2F}{3} - \frac{F}{3}+ma_M$
$Ma_M = F\cos\alpha - F$
$Ma_M = -F(1-\cos\alpha)$
$a_M = -\frac{F}{M}(1-\cos\alpha)$

Красный - крайняя степень сомнения в рассуждениях, особенно использование переносного ускорения.

Заранее благодарю.

[Oleg Zubelevich]

ну и что может быть неясно в такой задаче? неизвестны три скорости и одна сила натяжения. Я бы написал теорему о движении центра масс всей системы и два вторых закона Ньютона для малых тел+ кинематическое соотношение. Силы инерции еще зачем-то понадобились

[Pripyat]

Это школьная задача дана задолго до прохождения центра масс. И если можно её решить школьными методами, то хотелось бы узнать о них. Поэтому теорему о движении центра масс я пока использовать не могу, а всё остальное Вами описанное - могу.

[ewert]

Силы натяжения до и после каждого блока одинаковы. Маленькие грузики двигаются с одинаковыми ускорениями и потому двигаются так, как если бы просто скользили по горизонтальной плоскости под действием горизонтальной силы величины $F$, откуда и их ускорение $\frac{F}{3m}$ в любом случае. На большой же груз действуют две горизонтальные силы: вправо $F\cos\alpha$ со стороны правого конца нити и влево просто $F$ со стороны верхнего грузика (силы натяжения нити на учвстке между грузиками слева взаимно уравновешиваются), откуда опять же в любом случае его ускорение есть $\frac{F}M(\cos\alpha-1)$.

-- Ср окт 30, 2013 13:56:09 --

Это, разумеется, до тех пор, пока всё не опрокинется, т.е. пока $F\sin\alpha\leqslant(m+M)g$.

[Pripyat]

Т.е. так?


У меня остался только вопрос, верхний груз m никак не влияет на движение нижнего M? Нижний просто выскальзывает из под него? И даже как бы "не давит на него", не даёт массы?

[ewert]

Pripyat в сообщении #782127 писал(а):

верхний груз m никак не влияет на движение нижнего M? Нижний просто выскальзывает из под него? И даже как бы "не давит на него", не даёт массы?

Никак не влияет; но почему не давит-то? Давит, просто это не имеет никакого значения из-за отсутствия трения. Было бы трение -- имело бы.

[Pripyat]

ewert, большое спасибо. Теперь действительно понятно. Чего я там понагородил ...

[ewert]

Если грузики не двигаются относительно груза, то общее ускорение $a=\frac{F}{m_1+m_2+M}$. При этом верхний грузик движется горизонтально с тем же ускорением, а правый вертикально неподвижен, откуда $m_1a=T=m_2g$. Осталось исключить из этих двух уравнений ускорение.

[Oleg Zubelevich]

ewert в сообщении #782123 писал(а):

то, разумеется, до тех пор, пока всё не опрокинется, т.е. пока $F\sin\alpha\leqslant(m+M)g$.

вот это ,кстати, скорее всего вообще неверно

[nestoronij]

Pripyat в сообщении #782127 писал(а):

Т.е. так?


У меня остался только вопрос, верхний груз m никак не влияет на движение нижнего M? Нижний просто выскальзывает из под него? И даже как бы "не давит на него", не даёт массы?

Немного не так по рис. Не все силы изображены на нижние блоки, разве уж взялись.... Не вижу уравнений динамики..

[ewert]

Oleg Zubelevich в сообщении #783407 писал(а):

вот это ,кстати, скорее всего вообще неверно

Почему? Я несколько раз себя в этом месте перепроверял -- и ошибок не нашёл. Вернее, пару нашёл, но они сократились.

-- Пт ноя 01, 2013 23:28:38 --

nestoronij в сообщении #783418 писал(а):

Не все силы изображены на нижние блоки, разве уж взялись....

Все необходимые, остальное же праздно.

[Oleg Zubelevich]

при подъеме большой груз должен поворачиваться вокруг левого нижнего угла. Вы хотите сказать, что от размеров большого груза и от положения на нем маленького не будет зависеть сила при которой произойдет отрыв?

[ewert]

Я ничего не хочу сказать, кроме одного: ровно при этом условии суммарная вертикальная сила окажется направленной вверх -- и, следовательно, вся конструкция тем или иным способом, да опрокинется.

[Oleg Zubelevich]

подниматься она может и раньше начнет из-за рычага

[ewert]

(Оффтоп)

Oleg Zubelevich в сообщении #783429 писал(а):

подниматься она может и раньше начнет из-за рычага

это возможно (а может и нет), я об этом просто не задумывался. Во всяком случае, сила должна быть не слишком велика, в условии же это не оговорено. . И во всяком случае, необходимое-то условие я выписал честно. А достаточное выписать и невозможно -- оно зависит от положения верхнего грузика.