Analytic function construction

[anna.tomy]

Hello everyone,

Please, help to construct an analytic function f(z) that satisfies:
$f(it+2n)=\frac{\alpha}{2n}$
$f(it+2n+2)=\frac{\alpha}{2n+2}$
$f(\alpha)=1$,
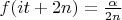
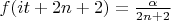
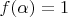
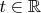
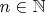
where $t\in \mathbb{R}$, $n\in \mathbb{N}$, $\alpha>0$ is such that $2n<\alpha<2n+2.$

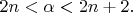
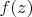
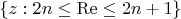
Shortly speaking, $f(z)$ is given on two boundaries of the strip $\{z:2n\leq\operatorname{Re}\le 2n+1\}$ and in one point on the real line of the strip.

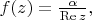
It seems to be $f(z)=\frac{\alpha}{\operatorname{Re} z},$ but it is not analytic.

If such function does not exist, please, then explain why.

Thanks in advance to everyone who will make any effort to help me.
Cheers

-- Чт окт 31, 2013 07:05:25 --

Please write in Russian if it is more convenient. I am Russian, just do not have Russian letters on my keyboard. Sorry....

-- Чт окт 31, 2013 07:10:19 --

It is even enough to assume that
$\operatorname{Re}f(it+2n)=\frac{\alpha}{2n}$
$\operatorname{Re}f(it+2n+2)=\frac{\alpha}{2n+2}$

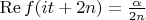
-- Чт окт 31, 2013 07:24:52 --

Sorry, I made a mistake:
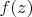
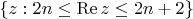
Shortly speaking, $f(z)$ is given on two boundaries of the strip $\{z:2n\leq\operatorname{Re} z\le 2n+2\}$ and in one point on the real line of the strip.

[anna.tomy]

I have found one linear function g(z) such that:
$\operatorname{Re} g(it+0)=\frac{\alpha}{2n}$
$\operatorname{Re} g(it+1)=\frac{\alpha}{2n+2}$
$g(\theta)=1$, for some $0<\theta<1$ that depends on $\alpha$
and I am trying to build the mapping from the strip $\{z:2n\leq\operatorname{Re} z \le 2n+2\}$ onto the strip $\{z:0\leq \operatorname{Re} z\le 1\}$
with a condition $\alpha\to\theta$, but I cannot do it.
It seems easy, it shoud be some drobno-linear function, isn't it?

[sup]

У Вас какая-то путаница. Не очень ясно речь идет об $f(z)$ или $\operatorname{Re} f(z)$.
Скорее всего второе. Таким образом Вам предлагают отобразить одну полосу на другую так, чтобы заданная точка $z = \alpha$ перешла в заданную $f(z) = 1$.
Это так или нет?

[anna.tomy]

Добрый день,

Задача свелась к тому что бы найти отображение $f(z)$ полосы $\{z:2n\le\operatorname{Re} z\le 2n+2\}$
на полосу $\{z:0\le\operatorname{Re} z\le 1\}$
такое чтобы $f(z)$ была аналитичной функцией в заданной полосе, чтобы границы переходили в границы
$\{\operatorname{Re} z=2n\}\to\{\operatorname{Re} z=0\}$
$\{\operatorname{Re} z=2n+2\}\to\{\operatorname{Re} z=1\}$
и кроме того
$f(\alpha)=\frac{(\alpha-2n)(n+1)}{\alpha}$
где $2n<\alpha<2n+2$, $n\in\mathbb N.$
Легко проверить, что $0<\frac{(\alpha-2n)(n+1)}{\alpha}<1$

-- Чт окт 31, 2013 12:10:34 --

sup в сообщении #782540 писал(а):

У Вас какая-то путаница. Не очень ясно речь идет об $f(z)$ или $\operatorname{Re} f(z)$.
Скорее всего второе. Таким образом Вам предлагают отобразить одну полосу на другую так, чтобы заданная точка $z = \alpha$ перешла в заданную $f(z) = 1$.
Это так или нет?

Да, задача именно такая.

[sup]

Ага, я так и подумал.
Ну тогда еще один вопрос. Вы намерены искать однолистное отображение или не обязательно?
Надо иметь в виду, что однолистное отображение полосы на полосу единственно с точностью до сдвига (как доказать? ). Поэтому легко проверить возможно оно или нет.
В общем случае предлагаю воспользоваться "эквивалентностью" полосы и плоскости с выколотой точкой (между ними есть конформное отображение)

[anna.tomy]

sup в сообщении #782570 писал(а):

Ага, я так и подумал.
Ну тогда еще один вопрос. Вы намерены искать однолистное отображение или не обязательно?
Надо иметь в виду, что однолистное отображение полосы на полосу единственно с точностью до сдвига (как доказать? ). Поэтому легко проверить возможно оно или нет.
В общем случае предлагаю воспользоваться "эквивалентностью" полосы и плоскости с выколотой точкой (между ними есть конформное отображение)

хотелось бы однолистное, но не обязательно
а как проверить существование однолистного отображения в данном случае?
Можно про общий случай тоже поподробнее?полосу в плоскость, потом плоскость сдвинуть и потом плоскость в полосу, как-то так?
какой функцией задается "эквивалентность" полосы и плоскости?

-- Чт окт 31, 2013 12:31:35 --

Думаю что функция $\frac{2z-2n}{2}$ и есть то самое однолистное отображение, но оно не переводит мою точку в нужную...

[sup]

Так, прошу прощения, но я, похоже, ввел Вас в заблуждение. В мои рассуждения закралась ошибка и пока я не могу предъявить такое отображение.
Насчет однолистного отображения. Пусть имеется некое однолистное отображение полосы на полосу. С помощью принципа симметрии его можно однолистно продолжить на всю плоскость. А таких отображений уже "не слишком много".