Hello everyone,
Please, help to construct an analytic function f(z) that satisfies:
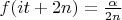
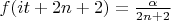
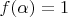
,
where
,
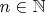
,

is such that
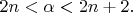
Shortly speaking,

is given on two boundaries of the strip
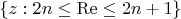
and in one point on the real line of the strip.
It seems to be
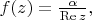
but it is not analytic.
If such function does not exist, please, then explain why.
Thanks in advance to everyone who will make any effort to help me.
Cheers
-- Чт окт 31, 2013 07:05:25 --Please write in Russian if it is more convenient. I am Russian, just do not have Russian letters on my keyboard. Sorry....
-- Чт окт 31, 2013 07:10:19 --It is even enough to assume that
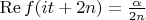
 -- Чт окт 31, 2013 07:24:52 --
-- Чт окт 31, 2013 07:24:52 --Sorry, I made a mistake:
Shortly speaking,

is given on two boundaries of the strip
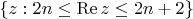
and in one point on the real line of the strip.



