science88, я не понял, Вы по Колокольчикову, что ли, теорию множеств изучаете? Выкиньте эту книжку куда-нибудь. Или сохраните до тех пор, когда начнёте понимать, что там бредятина написана, а пока не открывайте даже. Возьмите приличную книжку по теории множеств. Например:
П. С. Александров. Введение в теорию множеств и общую топологию.
К. Куратовский, А. Мостовский. Теория множеств.
Ну подробности как раз и интересуют. Так как нигде не нашел полного доказательства.
Если по Колмогорову, то разобьем наши подмножества на 2 класса B и G. У подмножеств B класса - дополнение бесконечно, у подмн. G - конечно.
(Оффтоп)
Суть дела в следующем.
Натуральный ряд — это множество положительных целых чисел

(в другой версии — неотрицательных целых чисел

; у Колмогорова и Фомина используется первый вариант).
Каждому подмножеству

натурального ряда можно сопоставить некоторое число из отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
по простой формуле

где

Наоборот, если задана двоичная запись числа
![$\alpha\in[0,1]$ $\alpha\in[0,1]$](https://dxdy-02.korotkov.co.uk/f/9/5/6/956cd791e512dfa01644376d1564b9f582.png)
, имеющая вид (1), то по ней восстанавливается соответствующее подмножество натурального ряда:

Причём, каждое число отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
имеет требуемую запись.
Проблема состоит, собственно, в том, что это соответствие является взаимно однозначным соответствием между подмножествами натурального ряда и записями вида (1), но не является взаимно однозначным соответствием между подмножествами натурального ряда и числами из отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Дело в том, что некоторые числа (они называются двоично-рациональными) имеют две записи вида (1), причём, в одна запись соответствует конечному подмножеству натурального ряда, а другая, наоборот, подмножеству с конечным дополнением (кроме чисел

и

, которые имеют только одну запись вида (1)).
Поэтому Колмогоров и Фомин разбивают все подмножества натурального ряда на два класса:

— те, которые имеют бесконечное дополнение (соответствующие записи (1) не могут оканчиваться бесконечной последовательностью

, так как содержат бесконечное число нулей), и
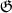
— те, которые имеют конечное дополнение (соответствующие записи (1) оканчиваются бесконечной последовательностью

, так как содержат лишь конечное число нулей).
Заметим, что формула (1) даёт взаимно однозначное соответствие между классом

и полуинтервалом

. Нужно только куда-то деть класс
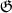
. Последовательность действий следующая.
1) Доказать, что класс
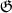
счётный. Для этого нужно перенумеровать конечные подмножества натурального ряда. Делается это просто. Попробуйте сами, потому что правила форума запрещают выкладывать решения простых учебных задач.
2) Доказать, что объединение счётного и конечного множества счётно.
3) Доказать, что объединение двух счётных множеств является счётным множеством.
4) Выбрать на полуинтервале

какое-нибудь счётное множество

и взаимно однозначно отобразить

на

.