Новое доказательство ВТФ для n=3

[Феликс Шмидель]

Сделаем замечание в оффтопике по леммам 6 и 7, которые играют важную роль в этой теме.

(Оффтоп)

Лемма 7 (являющаяся следствием леммы 6) позволила нам расширить множество простых чисел $q$, по модулю которых, число $x^2-\sqrt[3]{4} yz$ является квадратом в кольце $\mathbb{Z}[\sqrt[3]{2}]$ (сначала это множество содержало только такие $q$, по модулю которых, $\sqrt[3]{2}$ не существует).

Для доказательства лемм 6 и 7, важно не столько, чтобы число $x^6-4 (yz)^3$ было квадратом, как чтобы оно было квадратичным вычетом по модулю $q$ (где $q$ даёт остаток 2 по модулю 3 - речь идёт только о таких простых числах $q$).
В этом случае, возможно, что $x^2-s^2 yz$ не является квадратичным вычетом по модулю $q$ (где $s$ - такое натуральное число, что $s^3-2$ делится на $q$).
Тогда из леммы 7 следует, что $x^2-\sqrt[3]{4} yz$ не является квадратом в кольце $\mathbb{Z}[\sqrt[3]{2}]$.
Из леммы 6 следует, что $x^2-s^2 i_3 yz$ не сравнимо с квадратом в кольце $\mathbb{Z}[i_3]$.
Произведение $(x^2-s^2 i_3 yz)(x^2-s^2 i_3^2 yz)$ сравнимо с квадратом по модулю $q$ в кольце $\mathbb{Z}[i_3]$, но не в кольце целых чисел $\mathbb{Z}$.
Поэтому число $x^2-s^2 yz$ тоже сравнимо с квадратом по модулю $q$ в кольце $\mathbb{Z}[i_3]$, но не является квадратичным вычетом по модулю $q$.
Для примера, пусть $x=1$, $yz=2$ и $q=5$. В этом случае $s=3$.
Число $1^3-4 (2)^3=-31$ является квадратом по модулю 5, но $1-3^2 (2)=-17$ не является квадратичным вычетом по модулю 5.
В силу леммы 7, число $1-\sqrt[3]{4}(2)$ не сравнимо с квадратом по модулю 5 в кольце $\mathbb{Z}[\sqrt[3]{2}]$.

[Феликс Шмидель]

Получается, что мы не настолько ограничены в выборе множителя $\alpha(\sqrt[3]{2})$ для того, чтобы одно из чисел $x^2-\sqrt[3]{4} yz$ и $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ было представимо в виде $X^2+q Y^2$ (где $X, Y \in \mathbb{Q}[\sqrt[3]{2}]$).
Необязательно, чтобы норма числа $\alpha(\sqrt[3]{2})$ была квадратом (ранее мы брали $\alpha(\sqrt[3]{2})=\sqrt[3]{2}-1$ и $\alpha(\sqrt[3]{2})=y^2-\sqrt[3]{4} xz$, которые обладали этим свойством).
Достаточно, чтобы $\alpha(s)$ не было квадратичным вычетом по модулю $q$ (где $s$ - такое натуральное число, что $s^n-2$ делится на $q$), чтобы норма числа $\alpha(\sqrt[3]{2})$ была квадратичным вычетом по модулю числа $x^6-4 (yz)^3$ и, чтобы число $-q$ было квадратичным вычетом по модулю нормы числа $\alpha(\sqrt[3]{2})$.
Последнее условие гарантирует представимость числа $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ в виде $X^2+q Y^2$, где $X$ и $Y$ - $\rho$-адические числа для нечётных простых идеалов $\rho$, являющихся делителями нормы числа $\alpha(\sqrt[3]{2})$, а предпоследнее условие - для нечётных простых идеалов $\rho$, являющихся делителями числа $x^6-4 (yz)^3$.

[Феликс Шмидель]

Но из этого следует, что предпоследнее условие не является необходимым и достаточно первого и последнего условия, потому что они гарантируют, что число $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})$ представимо в виде $X^2+q Y^2$ для любых чисел $\alpha(\sqrt[3]{2})$ и $\beta(\sqrt[3]{2})$, удовлетворяющих этим двум условиям. Если теперь число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в виде $X^2+q Y^2$, то произведение $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде и, значит, число $\beta(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде.

[Феликс Шмидель]

Оформим эти новые идеи в строгом виде.
Сначала сформулируем по-новому леммы 6 и 7.
Дадим более простое доказательство леммы 6, подходящее и для общего случая простого показателя $n \ge 3$.

(Оффтоп)

В общем случае, пусть простые числа $q$ дают такой остаток при делении на $n$, который является генератором группы по умножению по модулю $n$.
Тогда полином $i_n^{n-1}+i_n^{n-2}+...+1$ неразложим на множители по модулю $q$, и в доказательстве лемм не будет принципиальных изменений.
При $n=3$, генерирующий остаток равен $2$.

Лемма 6А
-------------

Пусть $q$ - нечётное простое число, дающее остаток $2$ при делении на $3$.

Пусть $s$ - такое натуральное число, что $s^3 \equiv 2$ по модулю $q$.

Пусть $i_3$ - корень кубический из 1, отличный от 1.

Пусть число $v(\sqrt[3]{2})=a_0+a_1 \sqrt[3]{2}+a_2 (\sqrt[3]{2})^2$ (где $a_0$, $a_1$ и $a_2$ - целые числа), такое что:

(97) норма числа $v(\sqrt[3]{2})$ является ненулевым квадратичным вычетом по модулю $q$.

Число $v(s)$ является квадратичным вычетом по модулю $q$ тогда и только тогда, когда число $v(s i_3)$ сравнимо с квадратом в кольце $\mathbb{Z}[i_3]$ по модулю $q$.

Доказательство
---------------------

Заметим, что сравнение $X^3 \equiv 2$ по модулю $q$ имеет решение в целых числах, а сравнение $X^3 \equiv 1$ не имеет других решений в целых числах, кроме $X=1$ (иными словами, $\sqrt[3]{2}$ существует по модулю $q$, а $i_3$ не существует по модулю $q$).

Пусть $s$ - такое натуральное число, что $s^3 \equiv 2$ по модулю $q$.

Напомним, что нормой числа $v(\sqrt[3]{2})$ называется целое число, равное произведению $v(\sqrt[3]{2})v(\sqrt[3]{2} i_3)v(\sqrt[3]{2} i_3^2)$.
Запишем условие (97) в виде:

(98) $(v(\sqrt[3]{2})v(\sqrt[3]{2} i_3)v(\sqrt[3]{2} i_3^2))^{(q-1)/2} \equiv 1$ по модулю $q$,

Из (98) следует:

(99) полином $(v(X)v(X i_3)v(X i_3^2))^{(q-1)/2}-1-q f(X)$ делится на $X^3-2$,

где $f(x)$ - некоторый полином с целыми коэффициентами.

Подставляя $s$ вместо переменной $X$ в (99) получим:

(100) $(v(s)v(s i_3)v(s i_3^2))^{(q-1)/2} \equiv 1$ по модулю $q$.

Поскольку $v(s i_3^2) \equiv v(s i_3)^q$ по модулю $q$, то из (100) следует:

(101) $(v(s))^{(q-1)/2} (v(s i_3))^{(1+q)(q-1)/2} \equiv 1$ по модулю $q$.

Имеем:

(102) $v(s)$ является квадратичным вычетом по модулю $q$ тогда и только тогда, когда $(v(s))^{(q-1)/2} \equiv 1$ по модулю $q$.

Группа по умножению конечного поля $\mathbb{Z}_q[i_3]$ является циклической, порядка $q^2-1$ (иными словами, колличество элементов в группе равно $q^2-1$).
Поэтому:

(103) $v(s i_3)$ сравнимо с квадратом в кольце $\mathbb{Z}[i_3]$ по модулю $q$ тогда и только тогда, когда $(v(s i_3))^{(q^2-1)/2} \equiv 1$ по модулю $q$.

Из (101), (102) и (103) вместе следует:

(104) число $v(s)$ является квадратичным вычетом по модулю $q$ тогда и только тогда, когда число $v(s i_3)$ сравнимо с квадратом в кольце $\mathbb{Z}[i_3]$ по модулю $q$,

что и требовалось доказать.

[Феликс Шмидель]

Лемма 7А
-------------

Пусть $q$ - нечётное простое число, дающее остаток $2$ при делении на $3$.

Пусть $s$ - такое натуральное число, что $s^3 \equiv 2$ по модулю $q$.

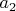
Пусть число $v(\sqrt[3]{2})=a_0+a_1 \sqrt[3]{2}+a_2 (\sqrt[3]{2})^2$ (где $a_0$, $a_1$ и $a_2$ - целые числа), такое что:

(105) норма числа $v(\sqrt[3]{2})$ является ненулевым квадратичным вычетом по модулю $q$.

Число $v(s)$ является квадратичным вычетом по модулю $q$ тогда и только тогда, когда число $v(\sqrt[3]{2})$ сравнимо с квадратом в кольце $\mathbb{Z}[\sqrt[3]{2}]$ по модулю $q$.

Доказательство
---------------------

Докажем сначала достаточность.
Пусть

(106) $v(\sqrt[3]{2}) \equiv (b_0+b_1 \sqrt[3]{2}+b_2 (\sqrt[3]{2})^2)^2$ по модулю $q$,

где $b_0$, $b_1$ и $b_2$ - целые числа.

Тогда:

(107) полином $v(X)-(b_0+b_1 X+b_2 X^2)^2 - q f(X)$ делится на $X^3-2$,

где $X$ - переменная, и $f(X)$ - некоторый полином с целыми коэффициентами.

Подставляя число $s$ вместо переменной $X$ в (107) получим:

(108) $v(s)-(b_0+b_1 s+b_2 s^2)^2$ делится на $q$.

Значит, число $v(s)$ является квадратичным вычетом по модулю $q$, что и требовалось.

Теперь докажем необходимость.

Пусть

(109) число $v(s) является квадратичным вычетом по модулю $q$.

Тогда

(110) число $v(s i_3)$ сравнимо с квадратом в кольце $\mathbb{Z}[i_3]$ по модулю $q$,

в силу леммы 6A.

Запишем (109) и (110) в виде:

(111) $v(s) \equiv b^2$ по модулю $q$,

(112) $v(s i_3) \equiv (b_0+b_1 i_3)^2$ по модулю $q$,

где $b$, $b_0$ и $b_1$ - целые числа.

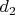
Найдём такие целые числа $d_0$, $d_1$ и $d_2$, чтобы выполнялись сравнения:

(113) $d_0+d_1 s+d_2 s^2 \equiv b$ по модулю $q$ и

(114) $d_0+d_1 s i_3+d_2 s^2 i_3^2 \equiv b_0+b_1 i_3$ по модулю $q$.

Поскольку $i_3^2=-1-i_3$, то сравнение (114) равносильно сравнениям:

(115) $d_0 - d_2 s^2 \equiv b_0$ по модулю $q$ и

(116) $d_1 s - d_2 s^2 \equiv b_1$ по модулю $q$.

Суммируя сравнения (115) и (116), получим:

(117) $d_0+d_1 s+d_2 s^2 - 3 d_2 s^2 \equiv b_0+b_1$ по модулю $q$.

Вычитая сравнение (117) из сравнения (113) получим:

(118) $3 d_2 s^2 \equiv b-b_0-b_1$ по модулю $q$.

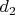
Из сравнения (118) можно найти $d_2$, и, затем, из сравнений (115) и (116) можно найти $d_0$ и $d_1$.

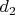
Таким образом, целые числа $d_0$, $d_1$ и $d_2$, удовлетворяющие сравнениям (113) и (114) существуют.

Пусть

(119) $v(\sqrt[3]{2}) - (d_0+d_1 \sqrt[3]{2}+d_2 (\sqrt[3]{2})^2)^2=e_0+e_1 \sqrt[3]{2}+e_2 (\sqrt[3]{2})^2$,

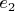
где $e_0$, $e_1$ и $e_2$ - целые числа.

Тогда

(120) полином $v(X) - (d_0+d_1 X+d_2 X^2)^2-(e_0+e_1 X+e_2 X^2)$ делится на $X^3-2$.

Подставляя $s$ вместо переменной $X$ в (120) и учитывая сравнения (111) и (113) получим:

(121) $e_0+e_1 s+e_2 s^2$ делится на $q$.

Подставляя $s i_3$ вместо переменной $X$ в (120) и учитывая сравнения (112) и (114), получим:

(122) $e_0+e_1 s i_3+e_2 s^2 i_3^2$ делится на $q$ в кольце $\mathbb{Z}[i_3]$.

Из (122) следует:

(123) числа $e_0-e_2 s^2$ и $e_1 s-e_2 s^2$ делятся на $q$.

Из (121) и (123) следует:

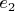
(124) числа $e_0$, $e_1$ и $e_2$ делятся на $q$.

Из (119) и (124) следует:

(125) число $v(\sqrt[3]{2})$ сравнимо с квадратом в кольце $\mathbb{Z}[\sqrt[3]{2}]$ по модулю $q$,

что и требовалось.

-- Пт май 31, 2013 18:40:00 --

Исправление:

Феликс Шмидель в сообщении #730540 писал(а):

Достаточно, чтобы $\alpha(s)$ не было квадратичным вычетом по модулю $q$ (где $s$ - такое натуральное число, что $s^n-2$ делится на $q$), чтобы норма числа $\alpha(\sqrt[3]{2})$ была квадратичным вычетом по модулю числа $x^6-4 (yz)^3$ и, чтобы число $-q$ было квадратичным вычетом по модулю нормы числа $\alpha(\sqrt[3]{2})$.

исправляется на:

Достаточно, чтобы норма числа $\alpha(\sqrt[3]{2})$ была квадратичным вычетом по модулю $q$, чтобы число $\alpha(s)$ не было квадратичным вычетом по модулю $q$ (где $s$ - такое натуральное число, что $s^n-2$ делится на $q$), чтобы норма числа $\alpha(\sqrt[3]{2})$ была квадратичным вычетом по модулю числа $x^6-4 (yz)^3$ и, чтобы число $-q$ было квадратичным вычетом по модулю нормы числа $\alpha(\sqrt[3]{2})$.

-- Пт май 31, 2013 18:46:43 --

Исправление
-----------------

Феликс Шмидель в сообщении #730603 писал(а):

Но из этого следует, что предпоследнее условие не является необходимым и достаточно первого и последнего условия, потому что они гарантируют, что число $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})$ представимо в виде $X^2+q Y^2$ для любых чисел $\alpha(\sqrt[3]{2})$ и $\beta(\sqrt[3]{2})$, удовлетворяющих этим двум условиям. Если теперь число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в виде $X^2+q Y^2$, то произведение $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде и, значит, число $\beta(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде.

исправляется на:

Но из этого следует, что предпоследнее условие не является необходимым и достаточно первых двух и последнего условия, потому что они гарантируют, что число $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})$ представимо в виде $X^2+q Y^2$ для любых чисел $\alpha(\sqrt[3]{2})$ и $\beta(\sqrt[3]{2})$, удовлетворяющих этим трём условиям. Если теперь число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в виде $X^2+q Y^2$, то произведение $\alpha(\sqrt[3]{2})\beta(\sqrt[3]{2})\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде и, значит, число $\beta(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде.

[Феликс Шмидель]

Можно и напрямую доказать, что достаточно первых двух и последнего условия для того, чтобы число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ было представимо в виде $X^2+q Y^2$, где $X, Y \in \mathbb{Q}[\sqrt[3]{2}]$.
Поэтому совсем необязательно искать число $\alpha(\sqrt[3]{2})$, чтобы оно удовлетворяло ещё и предпоследнему условию - в этом отношении, я перемудрил.
Не стоит также придавать такое большое значение леммам 6A и 7A (или 6 и 7).
Можно не ограничиваться только простыми числами $q$, дающими остаток $2$ при делении на 3.
Пусть $q$ даёт остаток 1 при делении на 3. Если $\sqrt[3]{2}$ не существует по модулю $q$, то мы знаем, что $x^2-\sqrt[3]{4} yz$ является квадратом в кольце $\mathbb{Q}[\sqrt[3]{2}]$ по модулю $q$.
Пусть $\sqrt[3]{2}$ существует по модулю $q$.
Поскольку $i_3$ тоже существует по модулю $q$, то числа $x^2-\sqrt[3]{4} i_3^{2k} yz$ существуют по модулю $q$, для любого $k=0, 1, ... n-1$.
Часть из них является квадратичными вычетами по модулю $q$, другая часть квадратичными невычетами.
Если числа $\alpha(\sqrt[3]{2} i_3^k)$ являются квадратичными вычетами по модулю $q$ для тех же индексов $k$, то число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ является квадратом в кольце $\mathbb{Q}[\sqrt[3]{2}]$ по модулю $q$. Наложив на число $\alpha(\sqrt[3]{2})$ дополнительное условие, чтобы его норма была представима в виде $X^2+q Y^2$, где $X, Y \in \mathbb{Q}[\sqrt[3]{2}]$, можно показать, что число $\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz)$ представимо в этом виде.
Что делать с этим дальше пока не ясно.

[Феликс Шмидель]

Мы начинаем исследовать решения уравнения: $X^2+q Y^2=\alpha(\sqrt[3]{2}) (x^2-\sqrt[3]{4} yz) Z^2$.


Лемма 15
-------------

Пусть $x^6-4 (yz)^3=a^2$, где $x$, $y$, $z$, $a$ - целые числа, $x$ - нечётное число, взаимно-простое с $yz$, и число $a$ не делится на 3.

Пусть $c=x^2-\sqrt[3]{4} yz$.

Пусть $q$ - такое простое число, нечётное и неравное 3-ём, что:

(126) $-q$ не является квадратичным вычетом по модулю любого из простых делителей числа $a$.

Пусть

(127) $X_1^2+q Y_1^2=\alpha c Z_1^2$,

где $\alpha$, $X_1$, $Y_1$ и $Z_1$ - ненулевые числа, принадлежащие кольцу $\mathbb{Z}[\sqrt[3]{2}]$.

Пусть

(128) правая часть равенства (127) делится на $\rho^k$,

где $\rho$ - простой идеал, являющийся делителем числа $c$, а $k$ - натуральное число.

Тогда числа $X_1^2$ и $Y_1^2$ делятся на $\rho^k$.

Доказательство:
---------------------

Достаточно доказать, что $Y_1^2$ делится на $\rho^k$, поскольку из этого утверждения, условия (128) и равенства (127) следует, что $X_1^2$ тоже делится на $\rho^k$.

Предположим:

(129) $Y_1^2$ не делится на $\rho^k$.

Пусть $\rho^{t}$ - наибольшая степень идеала $\rho$, на которую делится число $Y_1$.

В силу предположения (129), $2 t<k$.

Пусть $p$ - простое число, делящееся на $\rho$, и пусть $\beta \in \mathbb{Z}[\sqrt[3]{2}]$ - такое число этого кольца, которое делится на идеал $p/\rho$ и не делится на $\rho$.
Такое число $\beta$ cуществует, поскольку идеал $p/\rho$ не делится на $\rho$, так как $\rho$ не является ветвящимся, в силу того, что $6$ не делится на $\rho$.

Умножая равенство (127) на $\beta^{2 t}$ и деля на $p^{2t}$ получим:

(130) $X_2^2+q Y_2^2=u$,

где $X_2=\frac{X_1 \beta^t}{p^t}$, $Y_2=\frac{Y_1 \beta^t}{p^t}$, $u=\frac{\alpha c Z_1^2 \beta^{2t}}{p^{2 t}}$.

Из равенства (127) и того, что $Y_1$ делится на $\rho^{t}$ и $\alpha c Z_1^2$ делится на $\rho^{2 t}$ следует, что $X_1$ делится на $\rho^{t}$.
Поскольку $X_1$ делится на $\rho^{t}$, то $X_1 \beta^{t}$ делится на $p^{t}$, значит $X_2 \in \mathbb{Z}[\sqrt[3]{2}]$.
Поскольку $Y_1$ делится на $\rho^{t}$, то $Y_1 \beta^{t}$ делится на $p^{t}$, значит $Y_2 \in \mathbb{Z}[\sqrt[3]{2}]$.
Поскольку $\alpha c Z_1^2$ делится на $\rho^{2 t}$, то $\alpha c Z_1^2 \beta^{2t}$ делится на $p^{2 t}$, значит $u \in \mathbb{Z}[\sqrt[3]{2}]$.

Значит:

(131) числа $X_2$, $Y_2$ и $u$ принадлежат кольцу $\mathbb{Z}[\sqrt[3]{2}]$.

Поскольку $\rho^{t}$ - наибольшая степень идеала $\rho$, на которую делится число $Y_1$, то $Y_2$ не делится на $\rho$.
Поскольку $\alpha c Z_1^2$ делится на $\rho^{2t+1}$, то $u$ делится на $\rho$.
Значит:

(132) $Y_2$ не делится на $\rho$, $u$ делится на $\rho$.

Из равенства (130) и утверждений (132) следует:

(133) число $-q$ сравнимо с квадратом по модулю $\rho$ в кольце $\mathbb{Z}[\sqrt[3]{2}]$.

Запишем утверждение (133) в виде:

(134) $-q \equiv (v(\sqrt[3]{2}))^2$ по модулю $\rho$,

где $v(X)$ - квадратный полином с целыми коэффициентами.

Поскольку $c=x^2-\sqrt[3]{4} yz$ делится на $\rho$, то число $\sqrt[3]{4}$ сравнимо с $x^2/(yz)$ по модулю $\rho$, следовательно число $\sqrt[3]{2}$ сравнимо с $2 (yz)/x^2$ и из (134) следует:

(135) $-q \equiv (v(2 (yz)/x^2))^2$ по модулю $\rho$.

Из (135) следует:

(136) $-q \equiv (v(2 (yz)/x^2))^2$ по модулю $p$.

Сравнение (136) противоречит (126), значит предположение (129) неверно.
Что и требовалось.

[Феликс Шмидель]

Я вижу причину, по которой из равенства (127) трудно получить противоречие.
Дело в том, что существуют такие числа $g \in \mathbb{Z}[\sqrt[3]{2}]$, что число $g^2/c$ взаимно-просто с $c$, и $-q$ может быть квадратичным вычетом по модулю простых делителей нормы этого числа. Если, кроме этого, $\alpha c$ сравнимо с квадратом по модулю $q$ в кольце $\mathbb{Z}[\sqrt[3]{2}]$, то для таких $q$, уравнение:

(137) $X^2+q Y^2=\alpha (g^2/c) Z^2$

имеет ненулевые решения в кольце $\mathbb{Z}[\sqrt[3]{2}]$.

Помножив равенство (13) на $c^2$, получим ненулевые решения для уравнения:

(138) $X^2+q Y^2=\alpha c Z^2$.

Заметим, что $Z_1$ в (127) (или $Z$ в (138)) можно взять взаимно-простым с $c$.
В самом деле, если $Z_1$ делится на $\rho^k$, то, в силу леммы 15, $X_1$ и $Y_1$ тоже делятся на $\rho^k$, и, после умножения всех трёх чисел ($X_1$, $Y_1$ и $Z_1$) на $\beta^k$ (где число $\beta$ определено в доказательстве леммы 15), их можно сократить на $p^k$.

Но на этом, в исследовании решений уравнения (138), мы поставим точку, поскольку по указанной выше причине существование ненулевых решений этого уравнения ничему не противоречит.

[Феликс Шмидель]

Эти рассуждения дали мне новую идею: исследовать число $g^2/c$.
Для того, чтобы $g^2$ делилось на $c$, число $g$ должно принадлежать идеалу $(a, c)$, где $a^2=c d$ - норма числа $c$.
Если $g=u a+v c$, то

(139) $g^2/c=d u^2+2 a u v+c v^2$,

где $u$ и $v$ - произвольные числа кольца $\mathbb{Z}[\sqrt[3]{2}]$.

Правая часть равенства (139) является квадратичной формой с взаимно-простыми (не попарно) коэффициентами, которая принимает широкий спектр значений.

По предположению, дискриминант этой формы равен 0, хотя на самом деле, конечно, нет.

[Феликс Шмидель]

Разберём одну идею, связанную с равенством (140).
Покажем, почему она не ведёт к успеху, чтобы не отвечать на этот вопрос снова.

Рассмотрим представление правой части равенства (139) в виде

(140) $d u^2+2 a u v+c v^2=t_0+t_1 \sqrt[3]{2}+t_2 (\sqrt[3]{2})^2$,

где $t_0$, $t_1$ и $t_2$ - целые числа.

Если $t_1$ - нечётное число, то при умножении правой части равенства (140) на $c=x^2-\sqrt[3]{4} yz$ не получится квадрат (число вида $(b_0+b_1 \sqrt[3]{2}+b_2 (\sqrt[3]{2})^2)^2$) при нечётном $x$.
В самом деле, после раскрытия скобок в выражении $(t_0+t_1 \sqrt[3]{2}+t_2 (\sqrt[3]{2})^2)(x^2-\sqrt[3]{4} yz)$, коэффициент при $\sqrt[3]{2}$ был бы нечётным, а в выражении $(b_0+b_1 \sqrt[3]{2}+b_2 (\sqrt[3]{2})^2)^2$ - чётным.
Условие $t_1$ - нечётное число можно заменить на более общее: $t_1$ не делится на $2^{2 k+1}$, а все три числа $t_0$, $t_1$ и $t_2$ делятся на $2^{2 k}$ (где $k$ - какое-либо натуральное число).
Возможно, это условие можно удовлетворить при некотором выборе чисел $u$ и $v$, но мы не сможем это доказать, вот по какой причине.
Предположим $c \equiv 1$ по модулю 8. Тогда, согласно лемме 5, $c$ сравнимо квадратом в $\mathbb{Z}[\sqrt[3]{2}]$ по модулю $2^{2 k+1}$.
Заменяя в этом сравнении $\sqrt[3]{2}$ на $\sqrt[3]{2} i_3$ и на $\sqrt[3]{2} i_3^2$ и перемножая полученные сравнения для сопряжённых с $c$ чисел, получим, что
$d$ сравнимо квадратом в $\mathbb{Z}[\sqrt[3]{2}]$ по модулю $2^{2 k+1}$. Перемножая сравнения для $c$ и $d$, получим, что $c d$ сравнимо с квадратом целого рационального числа по модулю $2^{2 k+1}$.
Даже если равенство $c d=a^2$ невозможно, то сравнение $c d \equiv a^2$ по модулю $2^{2 k+1}$ вполне возможно (если говорить не о всех, а о каком-либо $k$).
Пусть $c \equiv X^2$, $d \equiv Y^2$ и $a \equiv X Y$ по модулю $2^{2 k+1}$. Тогда $d u^2+2 a u v+c v^2 \equiv Z^2$ по модулю $2^{2 k+1}$, где $Z=u X+v Y$.
Пусть $d u^2+2 a u v+c v^2$ делится на $2^{2 k}$. Тогда $Z$ делится на $2^k$ и $(d u^2+2 a u v+c v^2)/2^{2 k} \equiv (Z/2^k)^2$ по модулю $2$, поэтому условие $t_1$ не делится на $2^{2 k+1}$ не удовлетворяется.

[Феликс Шмидель]

Следующая идея, которую мы разберём: для каких чисел $\alpha \in \mathbb{Z}[\sqrt[3]{2}]$, уравнение:

(141) $d u^2+2 a u v+c v^2=\alpha w^2$,

c неизвестными $u$, $v$ и $w$, имеет ненулевое решение (с $w \ne 0$) в кольце $\mathbb{Z}[\sqrt[3]{2}]$.

Возьмём нечётный простой идеал $\rho$, на который не делятся $a$, $c$, $d$ и $\alpha$, и рассмотрим сравнение:

(142) $d u^2+2 a u v+c v^2 \equiv \alpha w^2$ по модулю $\rho$.

Согласно задаче 6 в параграфе 1 "Теории чисел" Боревича и Шафаревича, сравнение (142) всегда имеет ненулевое решение.
Однако ненулевого решения с $w \not \equiv 0$ по модулю $\rho$ может не быть.
При предположении $cd=a^2$ такое решение есть только если $c \alpha$ сравнимо с квадратом по модулю $\rho$ в кольце $\mathbb{Z}[\sqrt[3]{2}]$.
Несуществование такого ненулевого решения при других $\alpha$ хорошо иллюстрируется примером сравнения: $u^2+2 u v+ v^2 \equiv \alpha w^2$ по модулю простого числа $p$ в целых рациональных числах $u$, $v$ и $w$.

Таким образом идея, связанная с решением уравнения (141) для произвольных значений $\alpha$ не является перспективной.

Рассмотрим теперь другую идею: получить противоречие из того, что норма числа $d u^2+2 a u v+c v^2$ является квадратом при любых значения чисел $u$ и $v$ из кольца $\mathbb{Z}[\sqrt[3]{2}]$.
Это утверждение эквивалентно предположению: $c d=a^2$. Вопрос в том, можно ли выбрать числа $u$ и $v$ так, чтобы было проще получить противоречие?
Для простоты можно взять качестве $v$ произведение двух сопряжённых с $u$ чисел (в этом случае $u v$ - целое рациональное число). Может ли в этом случае $d u^2+c v^2$ быть целым рациональным числом?

[Феликс Шмидель]

Появилась ещё одна идея, связанная с предположением, что $cd=a^2$ (где $c=x^2-\sqrt[3]{4} yz$, $d=x^4-x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$ и $a$ -целое число.
Имеем: $d=x^4+x^2 (x^2-c)+(x^2-c)^2=3 x^4-3 x^2 c+c^2$, значит:

(143) $d=3 x^4-3 x^2 c+c^2$ и

(144) $c^3-3 x^2 c^2+3 x^4 c-a^2=0$

Предположим:

(145) $C^3-3 x^2 C^2+3 x^4 C-a^2 \equiv 0$ по модулю $p$,

где $C$ - целое число, и $p$ - простое число.

Тогда:

(146) $(c^3-3 x^2 c^2+3 x^4)-(C^3-3 x^2 C^2+3 x^4 C) $ делится на $p$.

Из (146) следует:

(147) $(c-C)(c-\frac{-(C-3 x^2)+(C-x^2) \sqrt{-3}}{2})(c-\frac{-(C-3 x^2)-(C-x^2) \sqrt{-3}}{2})$ делится на $p$.

Из (147) следует:

(148) $\sqrt[3]{2}$ существует по модулю $p$.

В самом деле, предположим:

(149) $\sqrt[3]{2}$ не существует по модулю $p$.

Тогда $p \equiv 1$ по модулю $3$, следовательно $i_3$ cуществует по модулю $p$, следовательно $\sqrt{-3}$ cуществует по модулю $p$.
Значит один из трёх сомножителей в (147) делится на $p$ и в любом случае $c$ сравнимо с целым числом по модулю $p$, откуда следует, что $\sqrt[3]{2}$ существует по модулю $p$, в противоречии с предположением (149).
Значит, предположение (149) неверно и утверждение (148) верно.

Остаётся доказать, что сравнение (145) возможно для какого либо целого $C$ и такого простого $p$, что $\sqrt[3]{2}$ не существует по модулю $p$.
Доказав это, мы сразу получили бы противоречие.

[Феликс Шмидель]

Кстати, если $\sqrt[3]{2}$ не существует по модулю $p$, то $a$ сравнимо с $(A^4-6 x^2 A^2 - 3 x^4)/(8 A)$ по модулю $p$, где $A$ - целое число.
Это нетрудно вывести из равенств (8) начала темы, если рассматривать их как сравнения по модулю $p$, и того, что $c$ сравнимо с квадратом по модулю $p$ в кольце $\mathbb{Z}[\sqrt[3]{2}]$.
Может быть это может помочь найти целое число $C$, удовлетворяющее сравнению (145)?

[Феликс Шмидель]

Феликс Шмидель в сообщении #732922 писал(а):

Я вижу причину, по которой из равенства (127) трудно получить противоречие.
Дело в том, что существуют такие числа $g \in \mathbb{Z}[\sqrt[3]{2}]$, что число $g^2/c$ взаимно-просто с $c$, и $-q$ может быть квадратичным вычетом по модулю простых делителей нормы этого числа. Если, кроме этого, $\alpha c$ сравнимо с квадратом по модулю $q$ в кольце $\mathbb{Z}[\sqrt[3]{2}]$, то для таких $q$, уравнение:

(137) $X^2+q Y^2=\alpha (g^2/c) Z^2$

имеет ненулевые решения в кольце $\mathbb{Z}[\sqrt[3]{2}]$.

Помножив равенство (13) на $c^2$, получим ненулевые решения для уравнения:

(138) $X^2+q Y^2=\alpha c Z^2$.

Заметим, что $Z_1$ в (127) (или $Z$ в (138)) можно взять взаимно-простым с $c$.
В самом деле, если $Z_1$ делится на $\rho^k$, то, в силу леммы 15, $X_1$ и $Y_1$ тоже делятся на $\rho^k$, и, после умножения всех трёх чисел ($X_1$, $Y_1$ и $Z_1$) на $\beta^k$ (где число $\beta$ определено в доказательстве леммы 15), их можно сократить на $p^k$.

Но на этом, в исследовании решений уравнения (138), мы поставим точку, поскольку по указанной выше причине существование ненулевых решений этого уравнения ничему не противоречит.

Я вижу в этом рассуждении изъян.
Конечно, если говорить о представимости числа $c=z^2-\sqrt[3]{4} xy$ в виде суммы двух квадратов, а точнее о равенстве

$X^2+Y^2=c Z^2$,

то идеалы $\rho$, на которые делятся простые числа вида $4t+3$, могут входить в разложение числа $c$ в чётных степенях, и в этом случае, это равенство, как мы показали, имеет место.
Но если $-q$ не является квадратичным вычетом по модулю любого простого делителя числа $z^6-4 x^3 y^3$, и это число не является квадратом (что мы хотим доказать), то число $g$, о котором шла речь не существует.
Предположим,

$X^2+q Y^2=c Z^2$,

где $Z$ является целым рациональным числом, взаимно простым с $z^6-4 x^3 y^3$, а $X$ и $Y$ принадлежат кольцу $\mathbb{Z}[\sqrt[3]{4}]$.
Из леммы 15 следует, что можно выбрать число $Z$ с указанными свойствами.
Из этого равенства можно вывести следствия относительно вида чисел $X$ и $Y$ по модулю простых делителей числа $z^6-4 x^3 y^3$.

[Феликс Шмидель]

Особенно простую форму по модулю $a$ (где $a^2=z^6-4 x^3 y^3$) имеют решения уравнения:

$X^2+q Y^2=d Z^4$,

где $d=z^4+z^2 xy \sqrt[3]{4}+ (\sqrt[3]{4} xy)^2$

Мы сейчас покажем, что $X$ и $Y$ сравнимы по модулю $a$ c $x_0 d$ и $y_0 d$, где $x_0$ и $y_0$ -целые рациональные числа.

Пусть

(150) $X_0^2+q Y_0^2=c Z^2$.

Заменяя в равенстве (150) $\sqrt[3]{4}$ на $\sqrt[3]{4} i_3$ и на $\sqrt[3]{4} i_3^2$, получим:

(151) $X_1^2+q Y_1^2=c_1 Z^2$ и

(152) $X_2^2+q Y_2^2=c_2 Z^2$.

Число $Z$ не меняется, поскольку мы выбрали его целым рациональным.
Умножая (151) на (152) получим:

(153) $X_3^2+q Y_3^2=d Z^4$,

где $X_3=X_1 X_2-q Y_1 Y_2$, $Y_3=X_1 Y_2+Y_1 X_2$.

Умножая (153) на (150) получим:

(154) $X_4^2+q Y_4^2=a^2 Z^6$,

где $X_4=X_0 X_3-q Y_0 Y_3$, $Y_4=X_0 Y_3+Y_0 X_3$, которые, как нетрудно показать, являются целыми рациональными числами.

Покажем, что $X_4$ и $Y_4$ оба делятся на $a$.
Если бы это было не так, то $X_4$ и $Y_4$ делились бы на одинаковую степень некоторого простого делителя $p$ числа $a$.
Сократив равенство (154) на эту степень $p$ (в квадрате) мы получили бы противоречие с тем, что $-q$ не является квадратичным вычетом по модулю $p$.

Таким образом, $X_0 X_3-q Y_0 Y_3$ и $X_0 Y_3+Y_0 X_3$ делятся на $a$,
откуда следует, что $(X_0^2+q Y_0^2) X_3$ и $(X_0^2+q Y_0^2) Y_3$ делятся на $a$.
Учитывая (150) получим: $c X_3$ и $c Y_3$ делятся на $a$

Поэтому $X_3$ и $Y_3$ сравнимы по модулю $a$ c $x_0 d$ и $y_0 d$, где $x_0$ и $y_0$ - некоторые целые рациональные числа.