А "из других классов" — это только

и

. Подумайте сами, почему. Там всё очевидно сразу, надо только написать вид чисел каждого класса.
Да, действительно, выписал, эти числа не будут простыми заведомо.

делится на 6.

делится на 2.

делится на 3.

делится на 2.
Все ли числа вида

являются простыми?
Разумеется, нет. Опять же, контрпримеры подберите сами, они небольшие и за минуту подбираются устно.
При

число
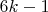
не будет простым.
Необходимо.
Из того, что

-- истинно, следует, что

-- простое.
Не выполняется необходимость. Контрпример

Достаточно.
Из того, что

-- простое следует истинность

Вот тут пока что мне не очевидно. Но есть предположение. Все простые числа, большие

, представимы в виде

. Ну а для

у меня уже получилось доказать делимость на 24. Верно?
Можно. Только опечатку исправьте.
