If I understand correctly, you start with any pandiagonal square (easy to constuct, e.g. with all numbers equal) and while keeping pandiagonality intact, change terms (N at a time) to arrive at distinct prime terms.
Jarekлукавите насчёт квадрата, состоящего из одинаковых чисел (если я правильно поняла перевод)?

Если мы возьмём пандиагональный квадрат, составленный из одинаковых чисел, то любое прибавление/вычитание одного и того же числа над элементами одной группы этого квадрата будет давать одинаковые числа в этой группе.
I think
Pavlovsky already explained this issue. Note that that is exactly the way one can construct, in case of prime

, pandiagonal square with consecutive integer entries:
Start with the pandiagonal square having all

terms equal to 0. Note that there are N groups of entries with N entries in each group - with no two entries of one group placed on the same line (row, column or broken diagonal). Add 1 to the first group, 2 to the second group, ..., N to N-th group. Then consider ANOTHER such split of terms of the square into N groups and add respectively 0,
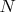
,

, ...,

to those groups. Then you arrive at a pandiagonal square composed of the consecutive integers ranging from 1 to

.
Whether we start the search with a square having all entries equal or with another pandiagonal square is not essential. I gave example of pandiagonal square with all entries equal as the starting square only to show that constructing initial pandiagonal square is not a difficult problem.
In case of prime N, we have

groups of terms, each group having N terms placed on distinct lines. There are 3 problems with that:
1. Number of groups is relatively small.
2. Number of terms in one group is relatively large. For example, for

each group has 17 terms - it is rather hard to force 17 numbers to be prime at the same time.
3. There is no simple way of applying this method to composite N.



