Правильным ли будет следующее доказательство утверждения: "При всяком движении полуплоскость переходит в полуплоскость"?
Пусть

- полуплоскость с границей

Выберем на прямой

две произвольные точки

и

Образами этих точек при движении будут точки

и

Проведём через точки

и

прямую

которая будет образом прямой

при принятом движении. Эта прямая будет границей образа

полуплоскости

при движении.
Возьмём в полуплоскости

произвольную точку

и опустим перпендикуляр

на прямую

а затем продолжим его неограниченно по другую сторону от точки

Получим луч

произвольной точке

которого соответствует её образ

на луче

такой, что

Каждому лучу, лежащему в полуплоскости
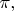
соответствует луч, лежащий в её образе

причём различным лучам соответствуют различные лучи (потому что движение является взаимно однозначным отображением плоскости на себя). Следовательно, образом полуплоскости

при движении является полуплоскость




