Спасибо за участие!!!
а). нет, это предположение не верно. O' может перемещаться произвольным образом.
б). да, каждое измерение состоит из трёх ординат y', точнее (0, y1'), (a, y2'), (a+b, y3'), так как в системе кооржинат x'O'y' абсциссы точек не изменяются.
Цитата:
От оси

до кривой или от кривой до оси

? Это не одно и тоже...
Можно считать что это одно и тоже в силу малости наклона касательной к кривой.
Проиллюстрирую данную ситуацию несколько инным, и кстати в силу малости углов поворота, эквивалентным способом. Имеем кривую K, и имеем отрезок AB, который обоими концами находится всегда на кривой, то есть образует хорду. Отрезок может перемещаться вдоль кривой, но таким образом, что всегда оба его конца принадлежат кривой. Объектом измерения в данной ситуации является расстояние от некотрой точки P, принадлежащей отрезку, до кривой K. В данном случае совместим ось X' с отрезком AB, точкe O' с A. Пусть |AP|=a и |PB|=b ( в предыдущем случае было a=b).
Несмотря на кажущиеся отличия, это представление эквивалентно предыдущему случаю, если заметить, что на основании измерений с трёх точек с абсциссами 0, a, (a+b) на произвольной оси X'' всегда можно расчитать расстояние от точки P до кривой с точностью до б.м. при условии малости угла между X'' и X и условии на кривую (f(x+a+b)-f(x)) << (a+b).
Если без картинки не очень понятно сейчас попробую это изобразить..

Вот картинка
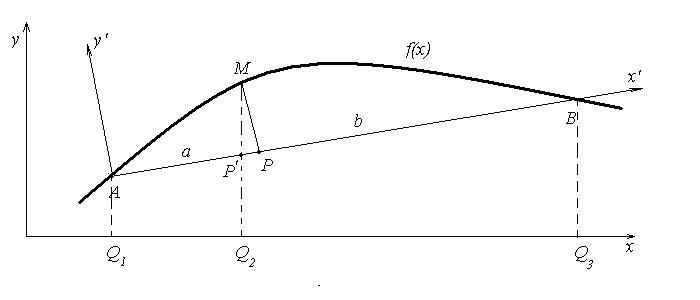
Принимаем, что MP' = MP, измеряемая величина - MP. Также эта величина может быть получена пересчётом как MP = y2' - y1'*a/(a+b) - y3'*b/(a+b), если осуществляются измерения относительно произвольной системы координат x'O'y', не привязанной к кривой и углол между x' и x небольшой.



