Задача, с решением которой возникла проблема, помещена в начале учебника по алгебре и аналитической геометрии, а не по теории чисел. В прошлом году решил эту задачу, но теперь не могу вспомнить, как я это сделал: "
Доказать, что если числа  и
и  взаимно просты, то существует натуральное
взаимно просты, то существует натуральное  , для которого
, для которого  делится на
делится на 
". Может быть, кто-нибудь предложит своё решение?
Возможно, следует рассмотреть некоторую последовательность чисел, дающих разные остатки при делении на

Среди

этих чисел обязательно найдутся такие, которые дают одинаковые остатки. Их разность делится на
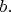
Эту разность нужно представить как произведение множителей, одним из которых является число вида

а другие множители не кратны
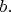
Как-то сложно получается...
Указанной задаче предшествуют три теоремы: о делении с остатком, о свойстве НОД двух чисел, о свойстве произведения двух взаимно простых чисел.