Задача:
Пусть

и

- натуральные числа, отличные от единицы, и такие, что

делится на

и
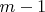
делится на

.
Доказать:

или

Вот ход моих рассуждений:
1) Начальные условия


По формуле разности кубов имеем:

Остаток произведения равен произведению остатков:



Очевидно что

Имеем:


имеем свойство

для любого натурального

применим его:


Перемножим два сравнения:

;

;

,

- целое.

;


т.к. при

дробь стремится к нулю при

.
Отношение

будет принимать натуральные значения только при

;

.
Вопросы:
1) Я чувствую, что неправомерно воспользовался свойствами произведения остатков.
2) Что делать со вторым? как доказать что

? Были мысли по поводу теоремы Эйлера, но не знаю как доказать взаимную простоту чисел.



