Как известно, универсальная обертывающая алгебра алгебры


получается посредством факторизации тензорной алгебры

по ее идеалу
![$$ I = a \otimes b - b \otimes a -[a,b]$$ $$ I = a \otimes b - b \otimes a -[a,b]$$](https://dxdy-01.korotkov.co.uk/f/4/5/1/45153802c53b25da9fe10cd9307bc50482.png)
.
Вопрос, собственно, простой:
а почему 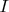 есть идеал
есть идеал 
? Если мы тензорно умножим элемент
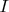
на произвольный элемент из

, мы никак не получим элемент из
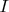
(антисимметричный тензор второго ранга + число), что требует понятие идеала.
Заранее спасибо.