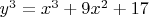
Надо найти все целые решения.
Я решил так: сначала доказал что

всегда будет нечетным. Взял случай когда и

и

нечетные и предположил что разница между ними 2, то есть

, и подставил в формулу:

. Получилось квадратное уравнение где 2 корня:

. В этом случае получается 2 решения:

и

.
Но как доказать что тут разница не может быть больше двух? Для четного

у меня решений не получилось.