Отборы команды Украины на международную олимпиаду 2007

[dm]

I тур

1. Для чисел $a$, $b$, $c$, больших $1/\sqrt{6}$ и удовлетворяющих условию $a^2+b^2+c^2=1$, доказать неравенство:

$$\frac{1+a^2}{\sqrt{2a^2+3ab-c^2}}+\frac{1+b^2}{\sqrt{2b^2+3bc-a^2}}+\frac{1+c^2}{\sqrt{2c^2+3ca-b^2}}\ge2(a+b+c).$$

2. У трапеции $ABCD$ с основаниями $AD$ и $BC$ угол между диагоналями прямой. Внутри $ABCD$ существует такая точка $M$, отличная от точки пересечения диагоналей, что $\angle AMB=\angle CMD=90^{\circ}$. Пусть $P$ — точка пересечения биссектрис углов $\angle A$ и $\angle C$, $Q$ — точка пересечения биссектрис углов $B$ и $D$. Доказать, что $\angle PMB=\angle QMC$.

3. Пусть $k$, $n$ — натуральные числа, удовлетворяющие условию $k+1\le\sqrt{\dfrac{n+1}{\ln(n+1)}}$. Докажите, что существует многочлен $P(x)$ степени $n$ с коэффициентами $1$, $0$, $-1$, делящийся на $(x-1)^k$.

II тур

4. Пусть $f$ — функция, действующая из множества рациональных чисел в множество рациональных чисел, такая, что:

$$f(x^2+y+f(xy))=3+(x+f(y)-2)f(x).$$

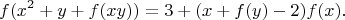
Найти все такие функции.

5. В остроугольном треугольнике $ABC$ проведены высоты $AA_3$ и $BB_3$, пересекающие описанную около треугольника окружность во второй раз в точках $A_1$ и $B_1$ соответственно. На прямых $BC$ и $AC$ выбраны такие точки $A_2$ и $B_2$, что $A_1A_2\parallel AC$ и $B_1B_2\parallel BC$. Точка $M$ — середина отрезка $A_2B_2$. Дано, что $\angle DCA=x$. Найти $\angle A_3MB_3$.

6. Простое число $p$ называется кубическим, если любое целое число представляется в виде $x^3+y^3+pz$, где $x$, $y$, $z$ — целые числа. Найти все кубические числа.

III тур

7. Из 25 человек любые двое разговаривают друг с другом на некотором языке, причем любые двое человек разговаривают друг с другом только на одном языке, даже если знают и другие общие языки. Известно, что среди любых трех человек найдется по крайней мере один, кто разговаривает с двумя другими из этих трех на одном и том же языке. Докажите, что найдется человек, разговаривающий на одном и том же языке с некоторыми 10 другими людьми.

8. Пусть многочлен $f(x)=x^4+a_1x^3+a_2x^2+a_3x+a_4$ с действительными коэффициентами имеет локальный максимум $M$ и абсолютный минимум $m$. Доказать, что

$$\frac{3}{10}\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2<M-m<3\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2.$$

9. Точки $A_1$, $B_1$, $C_1$ выбраны на сторонах $BC$, $CA$, $AB$ треугольника $ABC$ соответственно. Окружности, описанные около треугольников $AB_1C_1$, $BC_1A_1$, $CA_1B_1$, пересекают описанную около треугольника $ABC$ окружность в точках $A_2$, $B_2$, $C_2$ соответственно ($A_2\ne A$, $B_2\ne B$, $C_2\ne C$). Точки $A_3$, $B_3$, $C_3$ симметричны точкам $A_1$, $B_1$, $C_1$ относительно середин сторон $BC$, $CA$, $AB$ соответственно. Доказать, что треугольники $A_2B_2C_2$ и $A_3B_3C_3$ подобны.

IV тур

10. Для каких натуральных $n$ остроугольный треугольник $ABC$ с углом $\angle BAC<45^{\circ}$ можно разбить на $n$ вписанных четырехугольников, таких, что радиусы описанных около них окружностей образуют геометрическую прогрессию?

11. Имеется $n\ge2$ ламп $L_1,\ldots,L_n$, расположенных в ряд, каждая из которых может быть в одном из двух состояний — «вкл» или «выкл». Каждую секунду лампы одновременно меняют свое состояние по таким правилам: если лампа $L_i$ и ее соседи (при $i=1$, $i=n$ каждая лампа имеет ровно одного соседа, при других — двух) находятся в одинаковом состоянии, то она принимает состояние «выкл»; иначе она принимает состояние «вкл». В начальном положении все лампы находятся в состоянии «выкл», кроме самой левой лампы, имеющей состояние «вкл».
1) Доказать, что существует бесконечно много таких натуральных $n$, для которых все лампы будут со временем в состоянии «выкл».
2) Доказать, что существует бесконечно много таких натуральных $n$, для которых лампы не будут все одновременно в положении «выкл» ни в какой момент времени.

12. Доказать, что существует бесконечно много таких натуральных $n$, что все простые делители числа $n^3-1$ не превышают $\sqrt{n}$.

[RIP]

dm писал(а):

12. Доказать, что существует бесконечно много таких натуральных $n$, что все простые делители числа $n^3-1$ не превышают $\sqrt{n}$.

Возьмём серию решений уравнения Пелля $s^2-7d^2=8$, определённую формулой

$$s_k+d_k\sqrt7=(6+2\sqrt7)(8+3\sqrt7)^{Mk},\quad k\in\mathbb{N},$$

где число $M\in\mathbb{N}$ таково, что $(8+3\sqrt7)^M\equiv1\pmod{5\cdot7\cdot13}$, где сравнение рассматривается по модулю главного идеала $(5\cdot7\cdot13)$ в кольце $\mathbb{Z}[\sqrt7]$.

Если $n=d^4$, то

$$n^3-1=(d-1)\cdot7\cdot\frac{d^2+d+1}7\cdot(d+1)\cdot(d^2-d+1)\cdot5\cdot\frac{d^2+1}5\cdot(d^2-s+3)\cdot13\cdot\frac{d^2+s+3}{13}.$$

[student]

А кто нибуд решил первую задачу?

[juna]

dm писал(а):

I тур
6. Простое число $p$ называется кубическим, если любое целое число представляется в виде $x^3+y^3+pz$, где $x$, $y$, $z$ — целые числа. Найти все кубические числа.

Ясно, что $\forall n\in N:n-(x^3+y^3)\equiv 0 \mod p$, т.е. $(x^3+y^3)\mod p$ должно пробегать всю систему вычетов по этому модулю. Это означает, что не должно выполняться $x^3\equiv y^3\mod p$, т.е. $x^3\mod p$ должен пробегать всю систему вычетов. Извесно, что число $a$ является 3-степенным вычетом по модулю $p$, если $a^{\frac{p-1}{\text{НОД}(3,p-1)}}\equiv 1 \mod p$. Отсюда ясно, что если $\text{НОД}(3,p-1)=1$, то по теореме Ферма будем пробегать всю систему вычетов, в противном случае - нет.
Итак, простое число $p$ является кубическим тогда и только тогда, когда $3\not |(p-1)$

[maxal]

Артамонов Ю.Н. писал(а):

т.е. $(x^3+y^3)\mod p$ должно пробегать всю систему вычетов по этому модулю. Это означает, что не должно выполняться $x^3\equiv y^3\mod p$, т.е. $x^3\mod p$ должен пробегать всю систему вычетов.

Это неверно. Например, для $p=13$ числа $x^3+y^3$ пробегают всю систему вычетов, а вот $x^3$ - нет.

[juna]

Да, вы правы. Получается, что указанное условие является только достаточным. Сейчас, к сожалению, нет времени додумывать, но кажется, что начиная с некоторого $p$ все будут кубическими, т.к. число решений указанного сравнения, если $3|p-1$ будет $1+\frac{p-1}{3}$. Число сочетаний по 2 с повторениями от этого числа будет $\frac{(\frac{p-1}{3}+2)!}{2!{(\frac{p-1}{3})!}}$ и оно только для $p=7$ меньше 7, а дальше начинает расти и всегда существенно превышает $p$.

[RIP]

Все простые $p\ne7$ являются кубическими. Для $p\not\equiv1\pmod3$ это очевидно, поэтому в дальнейшем $p=6l+1$, $l\geqslant2$.
Воспользуемся теоремой Воспера (A. G. Vosper "The critical pairs of subsets of a group of prime order", J. London Math. Soc. 31 (1956), 200-205), из которой следует
Теорема. Пусть $p$ --- простое число, $A,B\subset\mathbb{Z}/p\mathbb{Z}$, $\min\{|A|;|B|\}\geqslant2$, $|A|+|B|<p$ ($|X|$ --- количество элементов множества $X$). Тогда либо $|A+B|\geqslant|A|+|B|$, либо $A$ и $B$ являются арифметическими прогрессиями с одной и той же разностью ($A+B:=\{a+b\mid a\in A,b\in B\}$).

Возьмём $A=B=\{x^3\mid x\in\mathbb{Z}/p\mathbb{Z}\}$, $|A|=2l+1$. A priori возможны 2 случая:

1) $|A+A|\geqslant|A|+|A|=4l+2$. Пусть $A_0:=A\setminus\{0\}$, $g$ --- п. к. по модулю $p$, $A_1:=gA_0$, $A_2:=g^2A_0$. Если $x\in A+A$, то для любого $y\in\mathbb{Z}/p\mathbb{Z}\qquad xy^3\in A+A$, следовательно, если $A_j\cap(A+A)\ne\varnothing$, то $A_j\subset(A+A)$ ($0\leqslant j\leqslant2$). Поскольку $|A+A|+|A_j|\geqslant(4l+2)+2l>p$ для каждого $j$, то отсюда получаем, что $A+A=\mathbb{Z}/p\mathbb{Z}$, т. е. число $p$ кубическое.

2) $A$ есть арифметическая прогрессия. Поскольку $0\in A$ и $A=-A$, то $A=\{-ld,-(l-1)d,\ldots,(l-1)d,ld\}$ для некоторого $d\in(\mathbb{Z}/p\mathbb{Z})^*$. Но тогда в $A$ лежат все $|k|\leqslant l$ (поскольку $k=(kd)/d$), т.е. $d=1$. Поскольку $l\geqslant2$, то $2\cdot l\in A$, но $2l$ не сравнимо по модулю $p$ ни с одним из $k$, $|k|\leqslant l$. Противоречие, т. е. этот случай невозможен.

[juna]

dm писал(а):

11. Имеется $n\ge2$ ламп $L_1,\ldots,L_n$, расположенных в ряд, каждая из которых может быть в одном из двух состояний — «вкл» или «выкл». Каждую секунду лампы одновременно меняют свое состояние по таким правилам: если лампа $L_i$ и ее соседи (при $i=1$, $i=n$ каждая лампа имеет ровно одного соседа, при других — двух) находятся в одинаковом состоянии, то она принимает состояние «выкл»; иначе она принимает состояние «вкл». В начальном положении все лампы находятся в состоянии «выкл», кроме самой левой лампы, имеющей состояние «вкл».
1) Доказать, что существует бесконечно много таких натуральных $n$, для которых все лампы будут со временем в состоянии «выкл».
2) Доказать, что существует бесконечно много таких натуральных $n$, для которых лампы не будут все одновременно в положении «выкл» ни в какой момент времени.

При $n=2$ легко получить, что все лампы придут в состояние "выкл". Легко понять, что "полному выключению" должно предшествовать состояние "полного включения". Т.е. для $n=2$ уже на первой итерации имеем все включены. Для любых дальнейших $n>2$ состояние все включено для $n=2$ уже всегда будет сохраняться. Оно должно повториться и в состоянии все включено и для $n>2$, т.е. в состояние все включено мы можем перейти только для таких $n$, которые делятся на $2$. Ближайшее будет $4$. Аналогично, состояние все включено будет повторяться и для $4$ и т.д. Окончательно получаем, что полностью выключаться будет в том и только в том случае, если $n$ является степенью $2$. Для других $n$ по итерациям должна наблюдаться некоторая фрактальная конструкция.

[Sasha Rybak]

Я по поводу 12-й задачи.

RIP писал(а):

Возьмём серию решений уравнения Пелля $s^2-7d^2=8$...

Зачем же так страшно? :)
Рассмотрим циклотомические многочлены (они же многочлены деления круга), определённые как: $\Phi_n(x)=\prod\limits_{k:\ 0\le k<n,\ \gcd(k,n)=1}(x-\varepsilon_n^k)$, где $\varepsilon_n=cos(2\pi/n)+i sin(2\pi/n)$ - первый корень n-й степени из единицы. По индукции несложно показать, что $\Phi_n(x)=\frac{(x^n-1)}{\prod_{d:\ d|n,\ 0<d<n}\Phi_d(x)}\ (n \in \mathbb N)$. Поэтому циклотомические многочлены обладают целыми коэффициентами, и при этом $deg(\Phi_n)=\varphi(n)$ - функция Эйлера от $n$.

Как известно, отношение $\frac{\varphi(3m)}{3m}$ может быть как угодно малым. Ну, по крайней мере меньше $1/6$ уж точно. :) Поэтому, взяв $n=x^{m}$ получим, что $n^3-1=x^{3m}-1$ разлагается в произведение циклотомических многочленов от $x$ степени $\varphi(3m)<m/2$, а также степеней $\varphi(d)\le\varphi(3m)<m/2$, где $d$ - делители $3m$. Для достаточно больших $x$ это и будет означать, что величина каждого множителя меньше $x^{m/2}=\sqrt n$.

[RIP]

Согласен, так намного проще.

[arqady]

dm писал(а):

1. Для чисел $a$, $b$, $c$, больших $1/\sqrt{6}$ и удовлетворяющих условию $a^2+b^2+c^2=1$, доказать неравенство:

$$\frac{1+a^2}{\sqrt{2a^2+3ab-c^2}}+\frac{1+b^2}{\sqrt{2b^2+3bc-a^2}}+\frac{1+c^2}{\sqrt{2c^2+3ca-b^2}}\ge2(a+b+c).$$

Да, это верно. Но я нашёл только некрасивое доказательство.

[Sasha Rybak]

Решил задачу 11.

Артамонов Ю.Н. писал(а):

Окончательно получаем, что полностью выключаться будет в том и только в том случае, если n является степенью 2.

Насчёт "в том случае" - согласен. А вот про "только в том случае" - неубедительно. :Ь Правда, исходя из процесса для $2^k$ ламп легко показать, что для $2^k+1$ ламп через $2^k$ шагов будет ситуация, симметричная ситуации после первого шага. Этого для решения задачи достаточно.

Хотя, на самом деле, можно доказать и для всех количеств, не равных степени 2. Моё решение выходит за рамки школьного курса. Тем не менее, рассказываю.

Будем рассматривать не сами лампы, а ОТЛИЧИЯ соседних ламп. То есть, если соседние лампы отличаются состоянием - то мы считаем, что отличие присутствует. Например, состоянию ламп 0011110 соответсвует "строка отличий" 010001.
По индукции легко доказать, что в "строке отличий" единички будут стоять на местах с ОДНОЙ ЧЁТНОСТЬЮ. (Если это выполнялось для исходного состояния, разумеется.) На основе этого просто получается следующая закономерность. На каждом следующем шаге в строке отличий k-тая цифра получается суммированием по модулю 2 (k-1)-й и (k+1)-й цифр в строке на данном шаге. Если цифры с номерами (k-1) или (k+1) отсутствуют, то считаем их равными 0.
Такое преобразование является ЛИНЕЙНЫМ над полем $F_2$. Ему соостветствует матрица
A=$\begin{pmatrix} 0&1&0&0&\ldots&0&0\\ 1&0&1&0&\ldots&0&0\\ 0&1&0&1&\ldots&0&0\\ 0&0&1&0&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&0&1\\ 0&0&0&0&\ldots&1&0\\ \end{pmatrix}$
размерности (n-1), где n - количество ламп.

Теперь рассмотрим ЦИКЛИЧЕСКУЮ строку длины 2n, которая преобразовывается по аналогичному правилу - цифра превращается в сумму двух её соседних цифр по модулю 2. Только теперь у КАЖДОЙ цифры есть две соседки. :) Этому преобразованию соответствует матрица
B=$\begin{pmatrix} 0&1&0&0&\ldots&0&1\\ 1&0&1&0&\ldots&0&0\\ 0&1&0&1&\ldots&0&0\\ 0&0&1&0&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&0&1\\ 1&0&0&0&\ldots&1&0\\ \end{pmatrix}$
размерности 2n, где n - количество ламп.
Начальным состоянием сделаем циклической строки сделаем $\vec w=\begin{pmatrix}0\\ \vdots\\0\\1\\ \end{pmatrix}$. Теперь по индукции доказываем, что $B^m \vec w=\begin{pmatrix}A^{m-1} \vec v \\ 0 \\ \mathrm{Sym}(A^{m-1} \vec v)\\0 \end{pmatrix}\ (m>0)$, где $\mathrm{Sym}$ означает симметричное отражение.
Поэтому вектор $A^m \vec v=\vec 0$ тогда и только тогда, когда $B^{m+1} \vec w=\vec 0$. Но если $B^r \vec w=\vec 0$, то $B^r \vec e_i=\vec 0$ для любого базисного вектора $\vec e_i$ - ведь $B$ коммутирует с циклическим сдвигом.
Но тогда $B^r=0$, а это возможно только в случае, когда все собственные числа оператора $B$ равны 0. Собственные числа - это корни уравнения $\det(B-\lambda I)=0$ относительно $\lambda \in F_{2^\infty}$ ($F_{2^\infty}$ означает алгебраическое замыкание поля $F_2$). В случае поля характеристики 2 минус можно заменить на плюс. :) Также сделаем замену $\lambda=\mu+\mu^{-1}$. Соответствующее $\mu \in F_{2^\infty}$ найдётся для любого $\lambda \in F_{2^\infty}$. Теперь вычислим определитель
$\det(B+\lambda I)=\begin{vmatrix} \mu+\mu^{-1}&1&0&0&\ldots&0&1\\ 1&\mu+\mu^{-1}&1&0&\ldots&0&0\\ 0&1&\mu+\mu^{-1}&1&\ldots&0&0\\ 0&0&1&\mu+\mu^{-1}&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu+\mu^{-1}&1\\ 1&0&0&0&\ldots&1&\mu+\mu^{-1}\\ \end{vmatrix}$.
Поскольку
$B+\lambda I=\begin{pmatrix} \mu+\mu^{-1}&1&0&0&\ldots&0&1\\ 1&\mu+\mu^{-1}&1&0&\ldots&0&0\\ 0&1&\mu+\mu^{-1}&1&\ldots&0&0\\ 0&0&1&\mu+\mu^{-1}&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu+\mu^{-1}&1\\ 1&0&0&0&\ldots&1&\mu+\mu^{-1}\\ \end{pmatrix}= \begin{pmatrix} \mu&1&0&0&\ldots&0&0\\ 0&\mu&1&0&\ldots&0&0\\ 0&0&\mu&1&\ldots&0&0\\ 0&0&0&\mu&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu&1\\ 1&0&0&0&\ldots&0&\mu\\ \end{pmatrix}+ \begin{pmatrix} \mu^{-1}&1&0&0&\ldots&0&1\\ 1&\mu^{-1}&0&0&\ldots&0&0\\ 0&1&\mu^{-1}&0&\ldots&0&0\\ 0&0&1&\mu^{-1}&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu^{-1}&0\\ 0&0&0&0&\ldots&1&\mu^{-1}\\ \end{pmatrix},$
то $\det(B+\lambda I)$ равен сумме определителей всех возможных матриц, в которых каждая строка выбирается или из первого, или из второго слагаемого в последней сумме. Но "смешанные" опеределители равны 0, поскольку они содержат пропорциональные строки. Значит,
$\det(B+\lambda I)= \begin{vmatrix} \mu&1&0&0&\ldots&0&0\\ 0&\mu&1&0&\ldots&0&0\\ 0&0&\mu&1&\ldots&0&0\\ 0&0&0&\mu&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu&1\\ 1&0&0&0&\ldots&0&\mu\\ \end{vmatrix}+ \begin{vmatrix} \mu^{-1}&1&0&0&\ldots&0&1\\ 1&\mu^{-1}&0&0&\ldots&0&0\\ 0&1&\mu^{-1}&0&\ldots&0&0\\ 0&0&1&\mu^{-1}&\ldots&0&0\\ \vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\ 0&0&0&0&\ldots&\mu^{-1}&0\\ 0&0&0&0&\ldots&1&\mu^{-1}\\ \end{vmatrix}=(\mu^{2n}+1)+(\mu^{-2n}+1)=\mu^{2n}+\mu^{-2n}.$
Множество собственных чисел равно $\{\mu+\mu^{-1}|\mu^{2n}+\mu^{-2n}=0\}=\{\mu+\mu^{-1}|\mu^{4n}=1\}$. Если n - не степень двойки, то подходит некоторое $\mu$, не равное 1. А для него соответствующее $\lambda$ не равно 0.

[juna]

Артамонов Ю.Н. писал(а):

Легко понять, что "полному выключению" должно предшествовать состояние "полного включения".

Из исходного состояния 1000.....0 можно переходить только в состояния с количеством включенных лампочек, равных степени двойки.
Отсюда следует, что

Артамонов Ю.Н. писал(а):

полностью выключаться будет в том и только в том случае, если $n$ является степенью $2$.

Артамонов Ю.Н. писал(а):

Для других $n$ по итерациям должна наблюдаться некоторая фрактальная конструкция.

1  0  0  0  0  0  0  0  0  0  
1  1  0  0  0  0  0  0  0  0  
0  1  1  0  0  0  0  0  0  0  
1  1  1  1  0  0  0  0  0  0  
0  0  0  1  1  0  0  0  0  0  
0  0  1  1  1  1  0  0  0  0  
0  1  1  0  0  1  1  0  0  0  
1  1  1  1  1  1  1  1  0  0  
0  0  0  0  0  0  0  1  1  0  
0  0  0  0  0  0  1  1  1  1  
0  0  0  0  0  1  1  0  0  0  
0  0  0  0  1  1  1  1  0  0  
0  0  0  1  1  0  0  1  1  0  
0  0  1  1  1  1  1  1  1  1  
0  1  1  0  0  0  0  0  0  0  
1  1  1  1  0  0  0  0  0  0  
0  0  0  1  1  0  0  0  0  0  
0  0  1  1  1  1  0  0  0  0  
0  1  1  0  0  1  1  0  0  0  
1  1  1  1  1  1  1  1  0  0  

- отражается от края

1  0  0  0  0  0  0  0  
1  1  0  0  0  0  0  0  
0  1  1  0  0  0  0  0  
1  1  1  1  0  0  0  0  
0  0  0  1  1  0  0  0  
0  0  1  1  1  1  0  0  
0  1  1  0  0  1  1  0  
1  1  1  1  1  1  1  1  
0  0  0  0  0  0  0  0  

- поглащается.

[Macavity]

Может кто-то решил задачу 8, хотелось бы увидеть решение. Я дошел до определенной точки, а дальше не знаю...

dm писал(а):

8. Пусть многочлен $f(x)=x^4+a_1x^3+a_2x^2+a_3x+a_4$ с действительными коэффициентами имеет локальный максимум $M$ и абсолютный минимум $m$. Доказать, что

$$\frac{3}{10}\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2<M-m<3\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2.$$

Примерно так.

Рассмотрим график этого многочлена. Какой у него вид - на минус бесконечности и плюс бесконечности он уходит в плюс бесконечность. Ближе к "центру" с обоих сторон находятся два минимума (один локальный, а один глобальный), а между минимумами находится один локальный максимум. Вот и всё.

Если этот график двигать вдоль осей X и Y, то значение выражения M-m не будет меняться. То есть это выражение есть инвариант при перемещениях графика.
Если менять величину a_4, то это будет соответствовать движению графика по вертикали настолько насколько будет меняться a_4. При этом остальные коеффициенты при движении по вертикали не меняются. Значит можно положить a_4=0, не уменьшая общности задачи.

Рассмотрим движение графика по горизонтали - оно достигается заменой вида y=x+a. При использовании такой замены выражение M-m остаётся инвариантом. Но здесь есть дополнительная проблема, при использовании такой подстановки меняются значения коэффициентов a_1, a_2 (a_4 тоже изменится, но это не принципиально так как движение по вертикали можно делать после движения по горизонтали). Нас однако больше беспокоит не столько значения этих коэффициентов сколько выражение

$$\frac{3}{10}\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2<M-m<3\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2.$$

.

Я обозначу \delta=\biggl(\frac{a_1^2}{4}-\frac{2a_2}{3}\biggr)^2. Собственно, я утверждаю, что это выражение есть инвариант при движениях по вертикали и горизонтали...
Возьмем вторую производную от многочлена и найдем точки перегиба графика:
x_{1,2}=-\frac{a_1}{4} \pm \frac{1}{2}{\sqrt{\frac{{a_1}^2}{4}-\frac{2a_2}{3}}}
Ясно, что расстояние по X между точками перегиба не меняется при перемещениях графика по вертикали и горизонтали. Значит \delta=(x_1-x_2)^4 - инвариант при перемещениях графика по горизонтали и вертикали.

Значит при решении без уменьшения общности можно рассматривать полином следующего вида: $f_1(x)=x^4+a_1x^3+a_2x^2$.

Про этот полином уже можно сказать, что он имеет один из экстремумов (локальный или глобальный) в точке x=0. Можно заметить, что если x_M - это место локального максимума для f_1, а также если в x=0 разместить глобальный минимум, то M-m=f_1(x_M)
(Вообще говоря, можно заметить, что существуют три различных движения по горизонтали, приводящие к a_3=0, по сути каждое из них совмещает положение одного из трех экстремумов по x с осью ординат).
Дальше вещи не столь важные, относящиеся к знакам a_1 и a_2. В частности можно ещё увидеть, что инвариантность \delta сохраняется при зеркальном отражении из x в -x.
Видно, что разница экстремумов оценивается четвертой степенью расстояния между точками перегиба с точностью до коэффициента... Фактически {$\frac {3} {10}}$ {\delta < f_1(x_M) < 3 \delta} .
Но что делать дальше непонятно - толи неравенство Йенсена (между точками перегиба функция выпукла вверх), толи что ещё. Может кто-то знает...? Спасибо..

Upd. Похоже я немного ошибся в x_{1,2}, дальше вроде все верно. Исправил.