Но т.к. количество вагонов нам заранее неизвестно, то начать лучше с единицы, а потом... надо подумать, или геометрическая прогрессия с коэффициентом 2 (и может минус 1), или какие-нибудь другие Фибоначчи
Я тоже к этому пришёл. И далеко не факт, что геометрическая прогрессия

, до которой легко догадаться - самая "быстрая" из всех последовательностей вообще. С ней у меня получилось

.
ЗЫ и, в частном случае, если не ошибаюсь, один длинный закольцованный в себя вагон определить нельзя
Конечно можно. Запоминаем свет в первом вагоне, идём во второй, там меняем, возвращаемся в первый. Если в первом тоже изменилось, то первый вагон=второй вагон.
Гасим первые 2 вагона. Потом возвращаемся назад и на обратном пути включаем. Если попался уже включенный, то мы нашли цикл. Потом повторяем то же со 4 вагонами, потом с 8 и т. д.
Количество операций будет не больше

Да, алгоритм верный. У меня примерно такой же алгоритм, только я шёл в

-ый вагон, менял там свет, возвращался в начальный и смотрел, поменялся ли где-нибудь ещё. Если поменялся, значит мы прошли поезд по кругу. Время получается

, если всегда возвращаться в первый и

, если в последней итерации уже не возвращаться в первый.
А вот с количеством операций
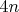
вы ошиблись. В наихудшем случае

получается как раз

, как и у меня, посмотрите.
Итак, остаётся открытым третий вопрос: можно ли сделать быстрее, чем за

(или за

, если я не прав и оценка
g______d всё-таки верная).
Если шагаем по геометрической прогрессии со знаменателем

, то

, минимум этой функции достигается как раз в точке

(что довольно любопытно).



