Предложите механизм размагничивания полем меньшим либо равным полю самого магнита.
Тогда и будет о чём дискутировать.
В обычных условиях - при соединении магнитов - размагничивания не происходит.
При соединении магнитов - поле не равно полю самого магнита, а меньше. Надо вставить магнит в ячейку из других магнитов, внутри которой создано такое же, но противоположное поле. Будет ли при этом размагничивание - не знаю.
Если смотреть на петлю гистерезиса, то как я понимаю, происходит следующее:
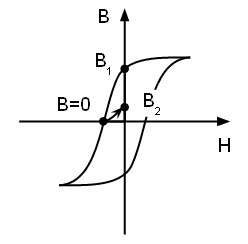
Изначально магнит намагничен до остаточного значения

Когда он входит в состав собранного шара, на него накладывается условие

Мы знаем, что движение по петле гистерезиса необратимо, и происходит по полной петле только в том случае, если внешнее приложенное поле меняется с размахом от максимума до минус максимума. Так что, после снятия условия

остаточная намагниченность не вернётся к значению

а примет какое-то меньшее значение

Детали эксперимента мне не известны. Видел рассказ об этом опыте сто лет назад на каком-то форуме в сети. Разговор там вообще шёл о другом, а этот факт упомянули мимоходом. Мне он показался интересным, поэтому запомнился. Как говорится, "за что купил, за то и продаю".
Тогда действительно, неизвестно, идёт ли речь об исчезновании магнитного поля или о размагничивании составляющих магнитов.
Ещё там упоминалось, что сферу нужно было удерживать от разрушения.
Значит, видимо, размагничивания составляющих магнитов не происходило, по крайней мере полного.
Впрочем, судя по вашей формулировке, возможно, удерживать надо было в процессе сборки, а не после него. Но это уже домыслы, а пока ваши воспоминания и скудная формулировка допускают и то, и другое.
Спасибо за подробности.
Все это на легенды похоже. Более менее предметно говорить можно, когда опыт опубликован, и не где-нибудь, а в рецензируемом журнале.
Что поделать, за неимением гербовой пишем на простой...
-- 17.04.2013 19:54:09 --Интересно, а в четырёх- и болеемерных пространствах, которыми играючи оперирует математика, найдётся ли возможность существования трёхмерного монополя? Наверняка там можно будет замкнуть поле - но я пока не готов это представить себе...
Разумеется, точно так же, как в трёхмерном пространстве может существовать цилиндр, из боковой поверхности которого линии поля торчат наружу: они просто входят внутрь через торец.